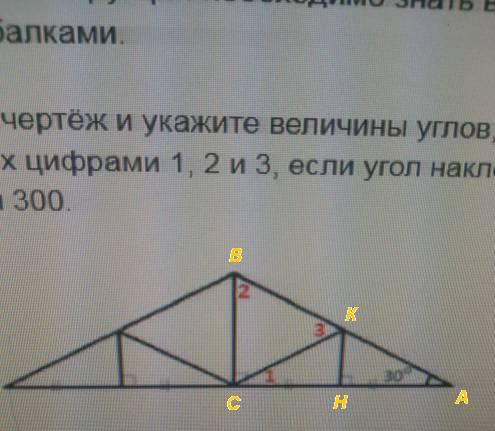
Для проверки конструкции необходимо знать величины углов между балками.Рассмотрите чертёж и укажите величины углов, обозначенных цифрами 1, 2 и 3, если угол наклона крыши равен 30°.

1 ответ

Посмотреть ответы

Megamozg

2180

Ответ:
∠1 = 30°
∠2 = 60°
∠3 = 60°
Объяснение:
Так как сумма острых углов прямоугольного треугольника равна 90°, то из ΔАВС:
∠АВС = 90° - ∠ВАС = 90° - 30° = 60°
∠2 = ∠АВС = 60°
В ΔАКС КН - высота и медиана, значит он равнобедренный. Углы при основании равнобедренного треугольника равны, значит
∠КСА = ∠КАС = 30°
∠1 = ∠КСА = 30°
∠ВКС - внешний угол треугольника АКС, значит равен сумме двух внутренних, не смежных с ним:
∠ВКС = ∠КАС + ∠КСА = 30° + 30° = 60°
∠3 = ∠ВКС = 60°

Хороший ответ

8 декабря 2022 17:42

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Дан треугольник BCE. Плоскость, параллельная прямой CE, пересекает BE в точке E1, а BC в точке C1. Найдите BC1, если C1 и E1 : CE = 3 : 8, BC = 28см р... Вершины А и С треугольника АВ C лежат в плоскости а. Через вершину В, не лежащую в плоскости А, проведена прямая, параллельная биссектрисе СМ треуголь... Прямые, содержащие биссектрисы внешних углов при вершинах B и C треугольника ABC, пересекаются в точке O. Найдите угол BOC, Если угол A равен а. Пож... Средняя линия равнобедренного треугольника,параллельная боковой стороне,равна 13 см,а медиана,проведенная к основанию 24 см. Найдите среднюю линию,пар... Объясните,какая дуга называется полуокружностью,какая дуга меньше полуокружности,а какая больше полуокружности?...