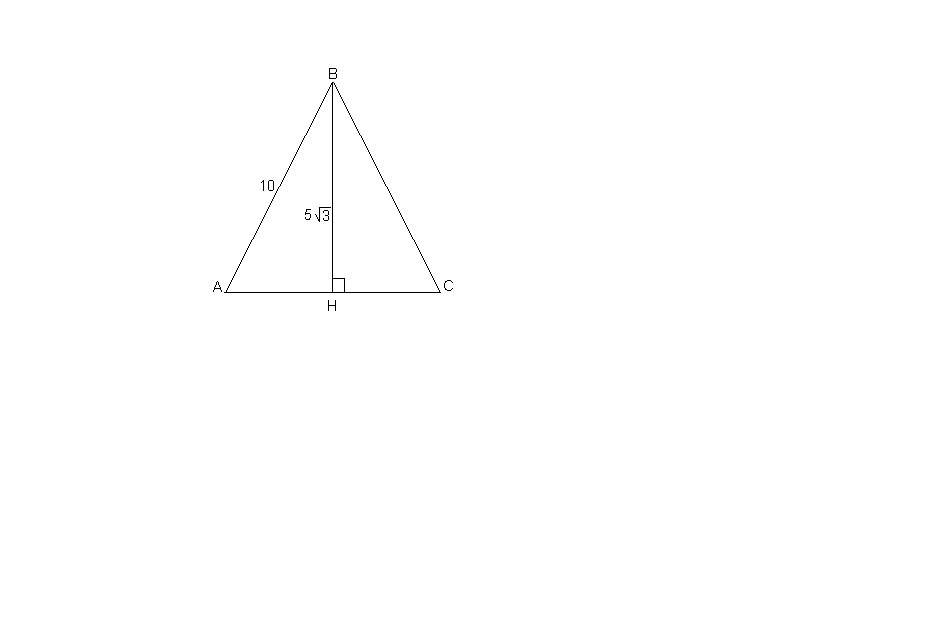
боковая сторона равнобедренного треугольника равна 10 см, а высота проведенная к основанию 5√3 см см,найти углы треугольника

1 ответ

Посмотреть ответы

Megamozg

2205

Способ 1.

Из прямоугольного треугольника ВАН:
sin ВАН = BH/AB = 5√3/10 = √3/2
Значит ∠ВАН = 60°.
∠ВСА = ∠ВАС = 60° как углы при основании равнобедренного треугольника.
∠АВС = 180° - 2·60° = 60°

Ответ: все углы треугольника по 60°.

Способ 2.

Из прямоугольного треугольника АВН по теореме Пифагора:
АН = √(АВ² - ВН²) = √(100 - 25·3) = √(100 - 75) = √25 = 5 см
Катет АН равен половине гипотенузы АВ, значит ∠АВН = 30°.
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой, тогда ∠АВС = 60°.

∠ВАС = ∠ВСА = (180° - 60°)/2 = 60°

Ответ: все углы треугольника по 60°.

Хороший ответ

8 декабря 2022 18:29

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Помогите!диагональ куба равна 6 см . Найдите: а)ребро куба б)косинус угла между диагональю куба и плоскостью одной из его граней. нужен чертёж и решен... Решите это пожалуйста) От точки K к прямой проведены перпендикуляр KB и наклонная KR. Определи расстояние от точки до прямой,если сумма... Определение прямоугольного треугольника,его элементы,обозначение.... Углы DEF и MEF - смежные, луч EK - биссектриса угла DEF, угол KEF в 4 раза меньше уг- ла MEF. Найдите углы DEF и MEF.... Найти точку пересечения прямой и плоскости (X-5)/2=(y+1)/3=(4-z)/11 Плоскость- x+5y-2z+1=0...