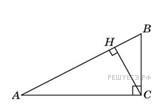
В треугольнике ABC угол C равен 90°, CH – высота, угол A равен 30° , AB=4. Найдите BH.

1 ответ

Посмотреть ответы

DevAdmin

1720

1) Так как ΔABC - прямоугольный, а катет BC лежит напротив ∠BAC в 30°, то:
BC = AB ÷ 2 = 4 ÷ 2 = 2
2) Так как ΔABC - прямоугольный, ∠BAC = 30°, то по теореме о сумме острых углов в прямоугольном треугольнике:
∠ABC = 90° - ∠BAC = 90° - 30° = 60°
Аналогично, ∠BCH = 30°
3) Так как ΔCHB - прямоугольный, а катет BH лежит напротив ∠HCB в 30°, то:
BH = BC ÷ 2 = 2 ÷ 2 = 1

Ответ: 1

Хороший ответ

8 декабря 2022 18:32

Остались вопросы?

Найти нужный

Еще вопросы по категории Алгебра

Павел въехал на участок дороги протяжённостью 2,7 км с камерами, отслеживающими среднюю скорость движения. Ограничение скорости на дороге – 60 км/ч.... 1. Выполните умножение: а) (а - 5) (а - 3); б) (5х + 4) (2х - 1); в) (3р + 2с) (2р + 4с); г) (6 - 2) (b2 + 2b - 3). • 2. Разложите на множители: а) х... Решить (2 sin (A-7П)+cos(3П/2)+A))/sin(A+П)... (1-sin^2(270+a))/(1-sin^2(180+a))... Пользуясь формулами приведения найдите a)tg120 b)tg150...