Лучшие помощники
- Megamozg 2180 б
- Matalya1 1800 б
- DevAdmin 1690 б
- arkasha_bortnikov 840 б
- Dwayne_Johnson 840 б
6 декабря 2022 18:34
1420
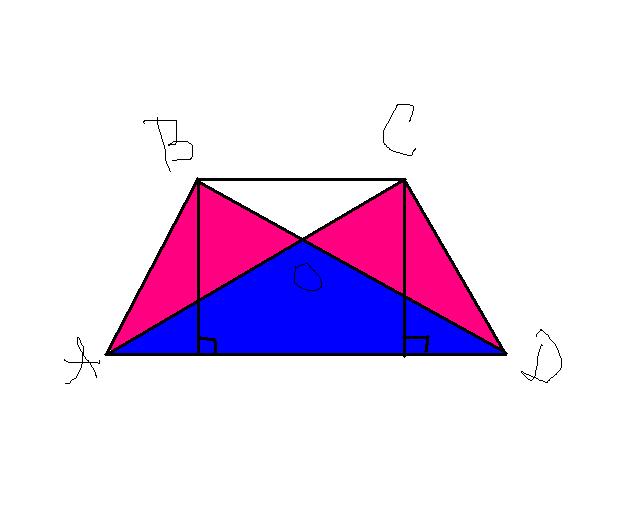
В трапеции ABCD c основаниями AD и BC диагонали пересекаются в точке О. Докажите , что площади треугольников AOB и COD равны.
1
ответ
Пусть AD - нижнее основание AD<BC
S(ABD)=S(ACD) - так как у єтих треугольников общее основание AD, а высоты треугольников, проведенные к основанию, являются высотами трапеции и потому равны.
S(AOB)=S(ABD)-S(AOD)
S(COD)=S(ACD)-S(AOD)
поєтому
S(AOB)=S(COD). Доказано
S(ABD)=S(ACD) - так как у єтих треугольников общее основание AD, а высоты треугольников, проведенные к основанию, являются высотами трапеции и потому равны.
S(AOB)=S(ABD)-S(AOD)
S(COD)=S(ACD)-S(AOD)
поєтому
S(AOB)=S(COD). Доказано
0
·
Хороший ответ
8 декабря 2022 18:34
Остались вопросы?
Еще вопросы по категории Геометрия
Прямые,содержащие высоты АА1 и ВВ1 треугольника АВС, пересекаются в точке Н, угол В- тупой, угол С=20 градусов. Найдите угол АНВ....
две сосны растут на расстоянии 30м одна от другой высота одной сосны 26м а другой 10м найдите расстояние между ихними верхушками развернутое решение п...
7класс № 255. В равнобедренном треугольнике CDE с основанием CE проведена высота CF. Найдите угол ECF,если угол D=54градуса...
катет прямоугольного треугольника равен 30 см а его проекция на гепотенузу 18 см найдите гипотенузу и второй катет треугольника...
Что такое определение (в геометрии)?...
Все предметы 
