Найти площадь сегмента круга,если R=6см,а центральный угол 120градусов ,и сделайте пожалуйста чертёж

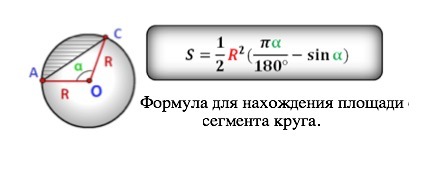
Для нахождения площади сегмента круга есть формула, - она дана в приложении, но мы можем вывести её сами, немного порассуждав.
Площадь круга S=πR²
Круг содержит 360° ⇒Площадь сектора круга в 1°=πR²:360
Площадь сектора с центральным углом α будет больше во столько раз, во сколько α больше 1.
Sсект=πR²•α:360°
Площадь сегмента АОС равна площади сектора АОС минус площадь треугольника АОС.
S ∆ AOC=AO•CO•sinα:2=R²•sinα:2 ( по одной из формул площади треугольника)
Вычитаем:
Sсегм. = πR²•α:360° - R²•sinα:2
Выносим за скобки R²1/2
Sсегм=R²•1/2•[(π•α:180°-sinα)]
Sсегм=(36:2)•[π•120°:180°-√3/2]
Sсегм=18•(3,14•120°:180°- √3/2)=18•[(3,14•2/3)-√3/2]
S сегм=18•(2,09- 0,866)= 18•1,224= ≈22,032 см²