Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
10 декабря 2022 12:30
1447
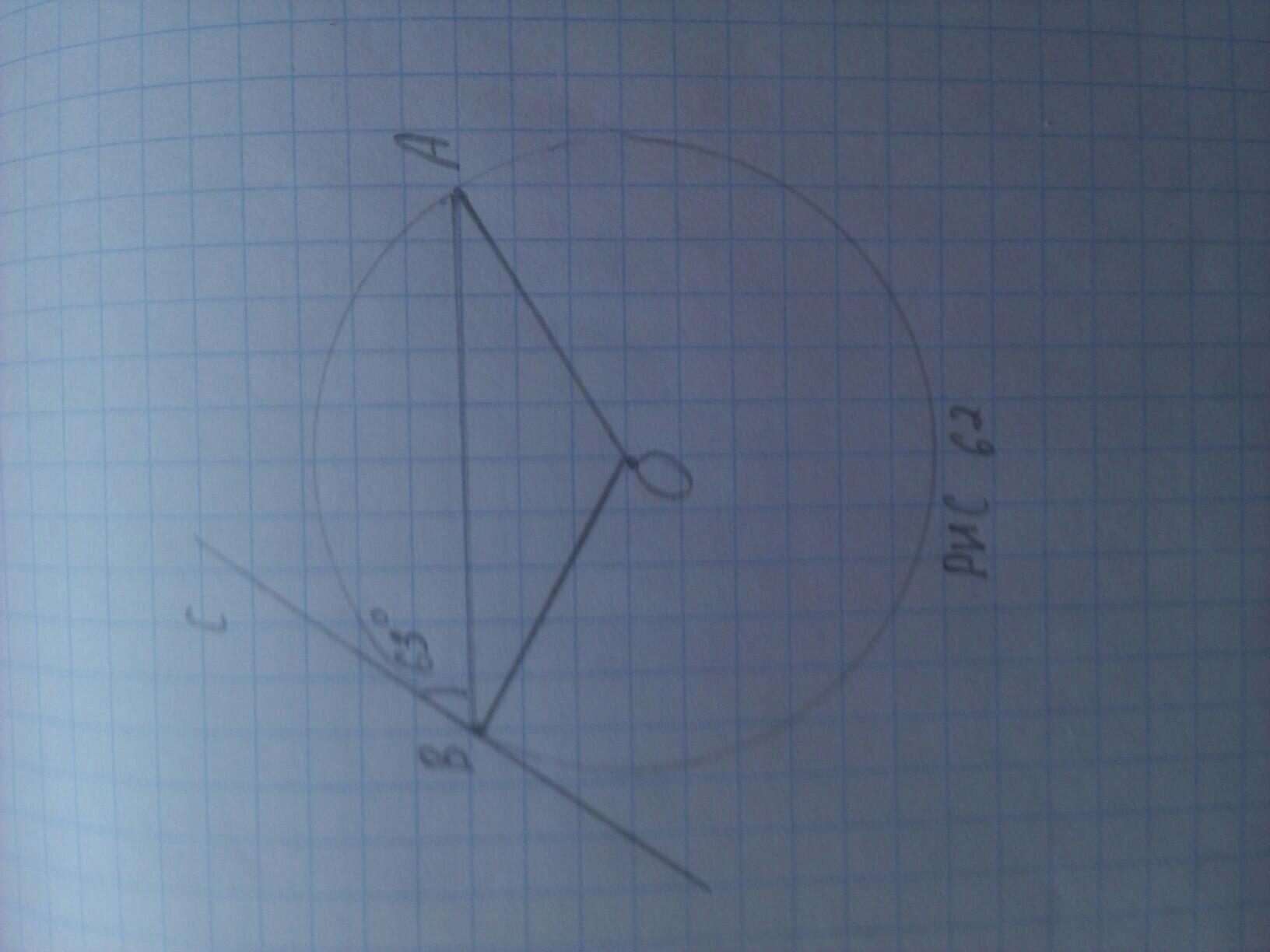
На рисунке 62 прямая ВС касается окружности с центром О в точке В. Найдите угол АОВ , если АВС= 63
2
ответа
Ответ:
∠AOB=126°
Объяснение:
По условию прямая BC касается окружности с центром O в точке B, что означает по определению касательной: прямая BC касательная к окружности.
По свойству касательной к окружности:
Касательная перпендикулярна радиусу, проведенному в точку касания.
Тогда ∠OBC = 90°, и следовательно ∠OBA = 90° - 63° = 27°.
Рассмотрим треугольник OBA с основанием AB. Так как стороны OA и OB треугольника являются радиусами, то ΔOBA равнобедренный. По свойству равнобедренного треугольника углы при основании равны, то есть ∠OAB = ∠OBA = 27°.
Сумма внутренних углов треугольника 180°:
∠OBA + ∠OAB + ∠AOB = 180°.
Отсюда
∠AOB = 180° - ∠OBA - ∠OAB = 180° - 27° - 27° = 126°.
∠AOB=126°
Объяснение:
По условию прямая BC касается окружности с центром O в точке B, что означает по определению касательной: прямая BC касательная к окружности.
По свойству касательной к окружности:
Касательная перпендикулярна радиусу, проведенному в точку касания.
Тогда ∠OBC = 90°, и следовательно ∠OBA = 90° - 63° = 27°.
Рассмотрим треугольник OBA с основанием AB. Так как стороны OA и OB треугольника являются радиусами, то ΔOBA равнобедренный. По свойству равнобедренного треугольника углы при основании равны, то есть ∠OAB = ∠OBA = 27°.
Сумма внутренних углов треугольника 180°:
∠OBA + ∠OAB + ∠AOB = 180°.
Отсюда
∠AOB = 180° - ∠OBA - ∠OAB = 180° - 27° - 27° = 126°.
0
12 декабря 2022 12:30
Остались вопросы?
Еще вопросы по категории Геометрия
В правильной треугольной пирамиде сторона основания равна 4 корня из 3см,а плоский угол при вершине равен 90 градусов .Найдите высоту пирамиды...
Квадрат это ромб у которого...... Квадрат это параллелограмм у которого диагонали...... Квадрат это четырехугольник у которого диагонали.........
Какие из следующих утверждений верны? 1) Вписанные углы окружности равны. 2) Через любые 3точки, не принадлежащие одной прямой, проходит единственная...
Что такое пифагоровы штаны...
Дан куб A…D1. Докажите перпендикулярность плоскостей: а) ABD и DCC1; б) AB1C1 и ABB1. Пожалуйста, решите подробно, ОБЯЗАТЕЛЬНО С ЧЕРТЕЖОМ. Если вы не...
Все предметы 
