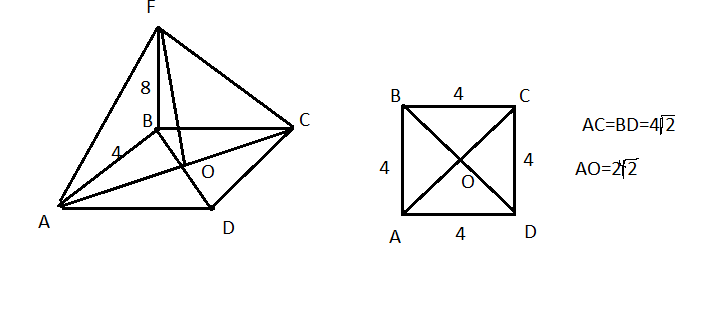
Через вершину В квадрата ABCD проведена прямая BF, перпендикулярная к его плоскости. Найдите расстояния от точки F до прямых, содержащих стороны и диагонали квадрата, если BF = 8 дм, АВ = 4 дм.

1 ответ

Посмотреть ответы

Megamozg

2205

См. рисунок в приложении
наклонная FA⊥ AD , так как её проекция ВА⊥AD
наклонная FO⊥AC , так как её проекция ВО ⊥ AC ( BD⊥AC- диагонали квадрата взаимно перпендикулярны)

По теореме Пифагора диагональ квадрата АС=√(4²+4²)=4√2
Диагонали квадрата в точке пересечения делятся пополам
АО=ОС=ВО=ОD=2√2

По теореме Пифагора из Δ AFB
AF²=AB²+FB²=4²+8²=16+64=80
AF=√80=4√5
Аналогично расстояние FC до стороны CD равно 4√5

По теореме Пифагора из Δ FBO
FO²=AO²+FB²=(2√2)²+8²=8+64=72
FO=√72=6√2

Расстояние до стороны АВ; ВС и диагонали BD равно FB=8

Хороший ответ

12 декабря 2022 14:30

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Напишите уравнение окружности с центром в точке С(2;1)проходящей через точку D(5;5)... Найти углы равнобедренного треугольника,если угол при основании равен 38 градусов.... Средние линии треугольника относятся как 2:2:4, а пириметр треугольника равен 45 см, найдите стороны треугольника... В правильной пятиугольной призме сторона основания равна 0,4 м, а высота равна 10 см. Вычислите площадь боковой и полной поверхности призмы.... 1)на отрезке ab взяты точки c а на отрезке cb -точка d. найдите длину отрезка bd если ab -15 см, cd -7 см, ac- 6 см. 2)На отрезке AB длиной 36 см взят...