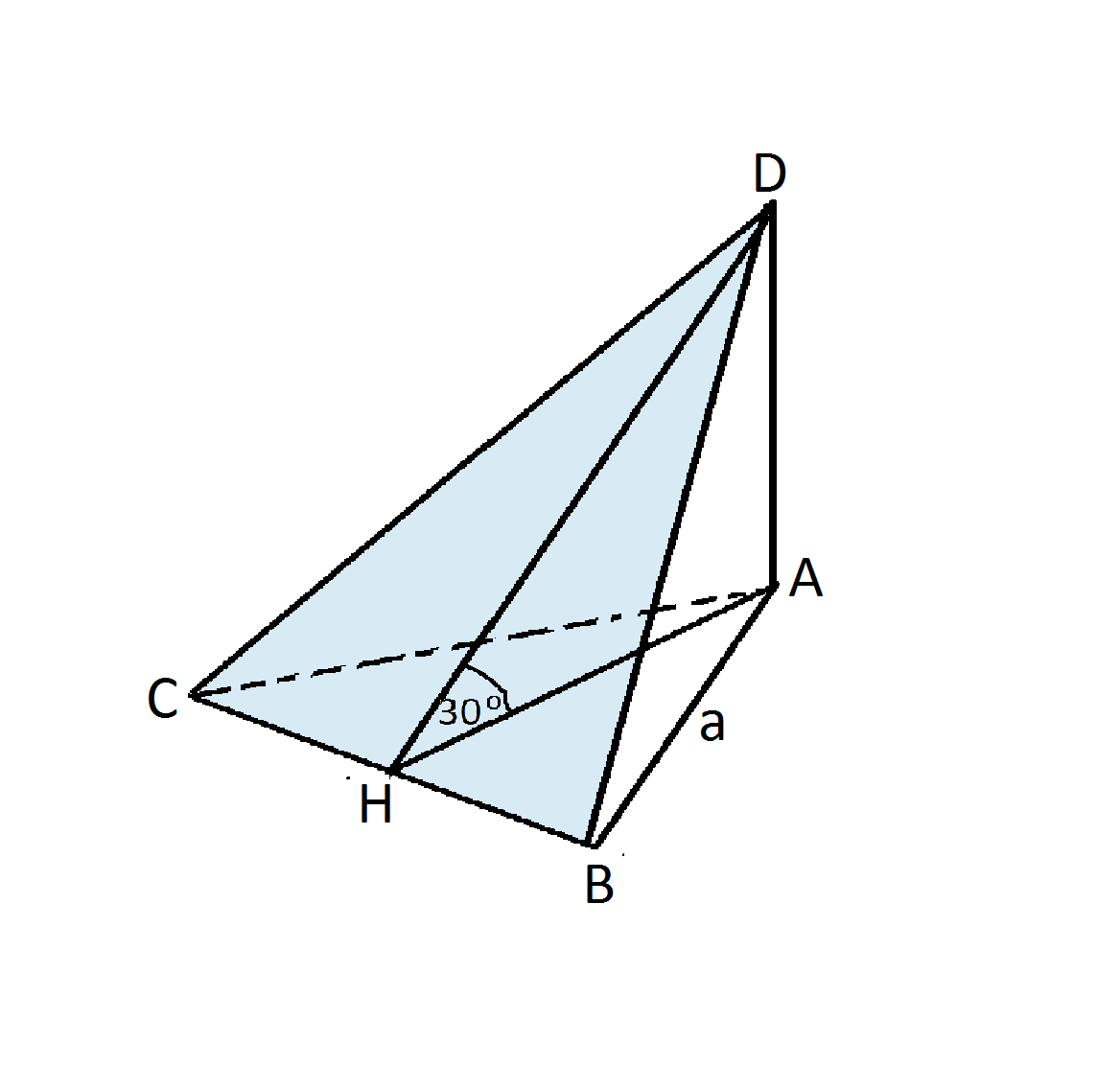
1. Основанием пирамиды DABC является правильный треугольник АВС, сторона которого равна а. Ребро DA перпендикулярно к плоскости АВС, а плоскость DBC составляет с плоскостью АВС угол в 30°. Найдите площадь боковой поверхности пирамиды.( с рисунком пожалуйста)

1 ответ

Посмотреть ответы

Megamozg

2205

Для решения задачи нужно знать
длину АD, DН и стороны основания,
синус и косинус 30°
АН- высота, медиана и биссектриса треугольника САВ
Треугольник в основании правильный, угол НАВ=60:2=30°
DН=АН:соs 30°
AH=AB*cos 30°=(а√3):2
DН=(а√3):2]:√3):2=а
DА=DН*sin 30°=а/2
Площадь боковой поверхности пирамиды состоит из суммы площадей
треугольника АDВ и 2-х равных треугольников САD и ВАD ( у них равны стороны).
S BDC=DH*CB:2= а*а:2=а²/2
SDAC+S DAB=2*AD*AB:2=2*а²:4=а²/2
Площадь боковой поверхности пирамиды:
S бок =а²/2+а²/2=а²

Хороший ответ

12 декабря 2022 18:05

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

В треугольнике MNK ∠M=66°, ∠N=54°, MK=50. Чему равна сторона NK?... Треугольники АВС и А1В1С1 подобны. ВС и В1С1, АС и А1С1- сходственные стороны..Найдите угол С, АВ и отношение площадей этих треугольников, если АС:А1С... Какое из следующих утверждений верно? 1) Площадь квадрата равна произведению двух его смежных сторон. 2) Диагональ трапеции делит её на два равны... в правильной четырехугольной пирамиде sabcd с основанием abcd боковое ребро sa равно 5,сторона основания равна 4в корне2. найдите объем пирамиды.... в прямоугольном треугольнике ABC угол С= 90 градусов,угол А=30 градусов, ВС= 12 в квадратном корне 2.Найдите гипотенузу Срочно,заранее спасибо...