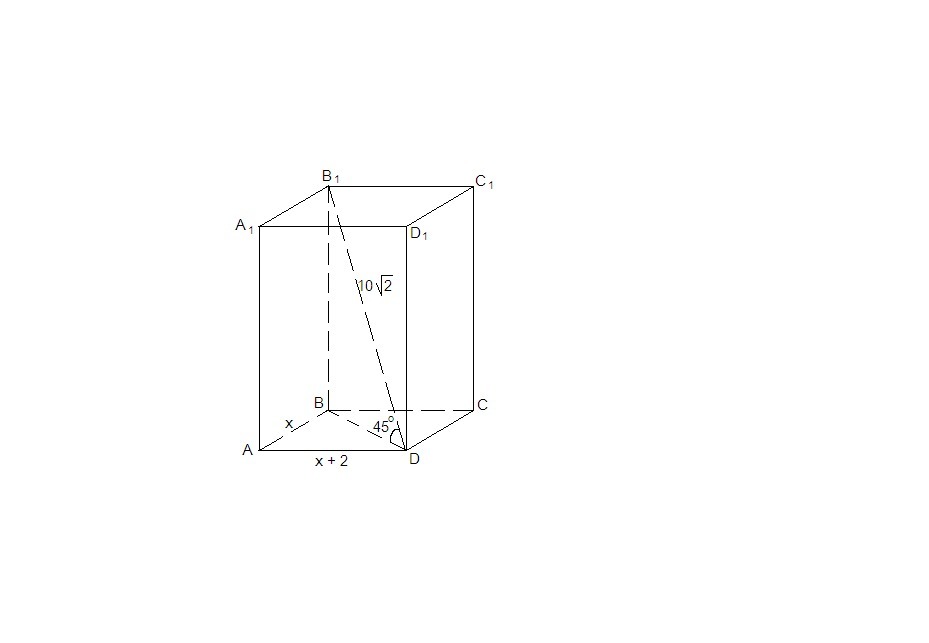
Диагональ прямоугольного параллелепипеда равна 10 корней из двух (см) и образует с плоскостью основания 45 градусов.Найти объем параллелепипеда,если одна сторона основания на 2см больше другой.

1 ответ

Посмотреть ответы

Megamozg

2205

Все грани прямоугольного параллелепипеда - прямоугольники. ВВ₁⊥(АВС)⇒
BD - проекция диагонали В₁D на плоскость основания. Тогда ∠В₁DB = 45°.
ΔВ₁DB прямоугольный и, значит, равнобедренный.
BD = BВ₁ = В₁D/√2 = 10 cм

ΔABD:
∠BAD = 90°. Пусть АВ = х, тогда AD = х + 2. По теореме Пифагора
BD² = AB² + AD²
100 = x² + (x + 2)²
2x² + 4x - 96 = 0
x² + 2x - 48 = 0
x = 6 или х = - 8 по теореме Виета
По смыслу задачи подходит х = 6
АВ = 6 см, AD = 8 см.
V = AB · AD · AA₁ = 6 · 8 · 10 = 480 cм³

Хороший ответ

16 декабря 2022 21:20

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Хорда перпендикулярна к диаметру и делит его на отрезки 4 см и 16 см. Определи длину хорды.... Какое из следующих утверждений верно? 1) Диагонали параллелограмма равны. 2) Площадь ромба равна произведению его стороны на высоту, проведённую к э... По координатам вершин треугольника ∆ABC найти: • уравнение линии BC ; • уравнение высоты AK ; • длину высоты AK ; • уравнение прямой (l), которая п... В треугольнике АВС со сторонами AB = 2, AC = 3, биссектриса AL и медиана BM пересекаются в точке K. Найдите: а) отношение BK : KM ; б) отношение площ... помогите! Задача. Из некоторой точки проведены к данной плоскости перпендикуляр и наклонная угол между которыми равен фи. Найдите перпендикуляр и прое...