Лучшие помощники

Megamozg 2200 б
Matalya1 1800 б
DevAdmin 1705 б
arkasha_bortnikov 895 б
Dwayne_Johnson 860 б

Показать еще

·

Геометрия

14 декабря 2022 23:31

1084

Найти катеты прямоугольного треугольника,если гипотенуза равна 4 см,а косинус одного из углов 0,6.

2 ответа

Посмотреть ответы

Ответ:
2,4 см и 3,2 см.
Объяснение:
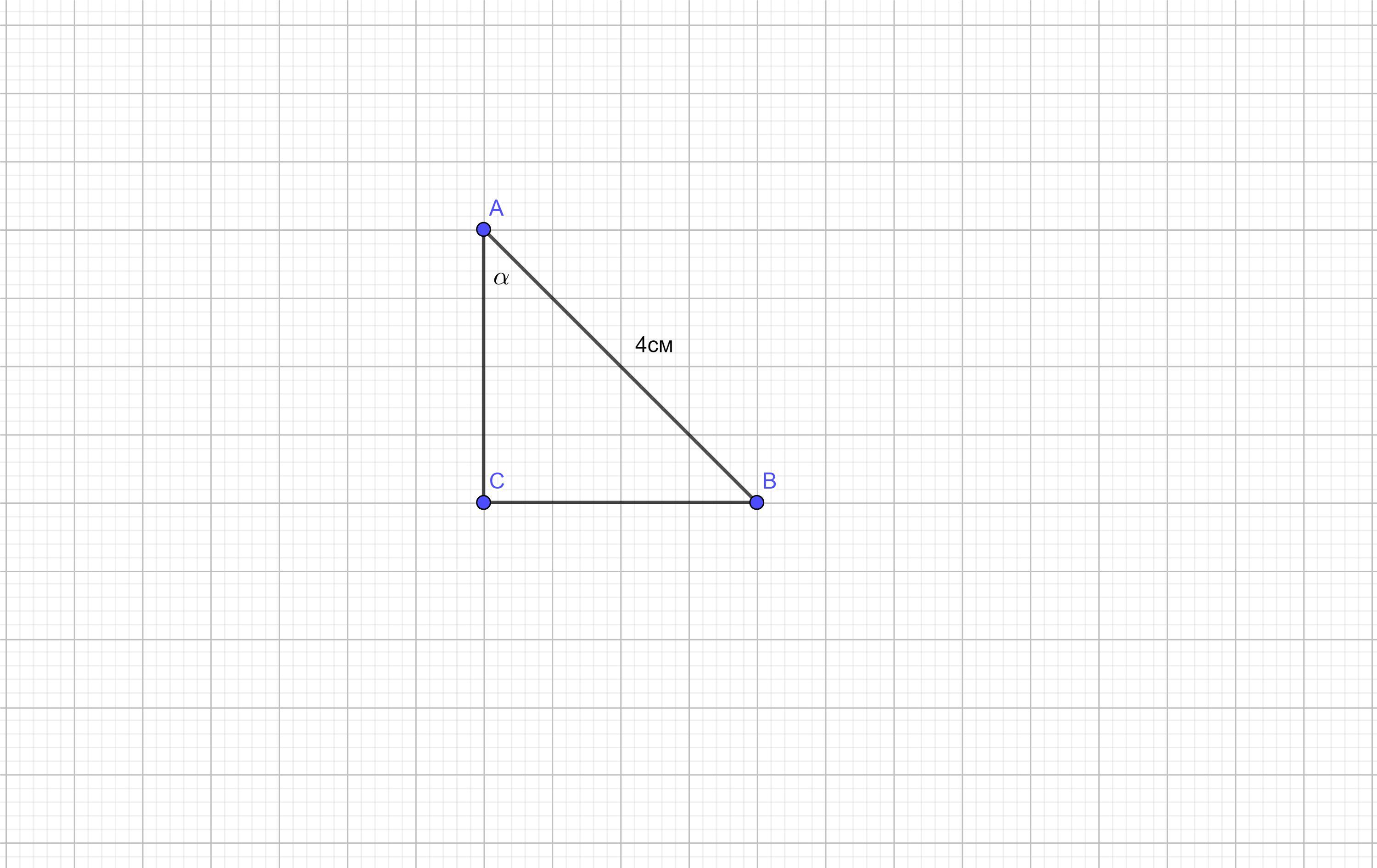
ΔABC- прямоугольный ,
∠C=90°, ∠A=α, cos α=0,6.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
$cos\alpha = \frac ;\\AC= AB*cos\alpha ;$
$AC= 4*0,6= 2,4$ см.
Найдем катет BC по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
$AB^ =AC^ +BC^ ;\\BC^ = AB^ - AC^ ;\\BC= \sqrt-AC^ } ;\\BC= \sqrt -2,4^ } =\sqrt =\sqrt =3,2;$
BC= 3,2 см.

0

·

Хороший ответ

16 декабря 2022 23:31

Дано :

ΔАВС - прямоугольный (∠В = 90°).
АС = 4 см, cos(∠С) = 0,6.

Найти :

АВ = ?, ВС = ?

Решение :

Косинус острого угла прямоугольного треугольника - это отношение прилежащего катета к гипотенузе.

Следовательно, $cos(\angle C) = \frac$
$0,6 = \frac \\\\BC = 0,6*4~cm = 2,4~cm.$

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

Следовательно, AC² = AB² + BC² ⇒ AB² = AC² - BC² ⇒ АВ = $\sqrt -BC^ } = \sqrt-2,4^ } = \sqrt =\sqrt = 3,2~cm.$

Ответ :

3,2 см, 2,4 см.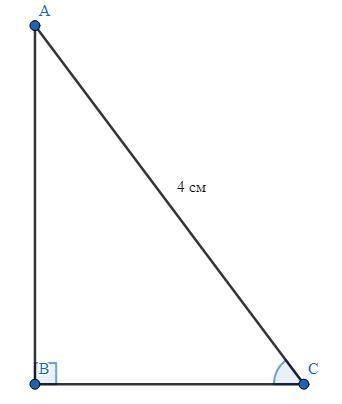

0

16 декабря 2022 23:31

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

В квадрат вписана окружность. Найдите отмеченный на рисунках угол. https://postimg.cc/2qfvmBY0... На какие два угла нельзя разбить тупой угол лучом выходящим из его вершины... Свойства четырехугольников... Треугольник авс равнобедренный , ав= вс= 6 см ас=8см найти площадь и радиус вписанной окружности... В угол С величиной 107 вписана окружность, которая касается сторон угла в точка A и B найдите угол aob...