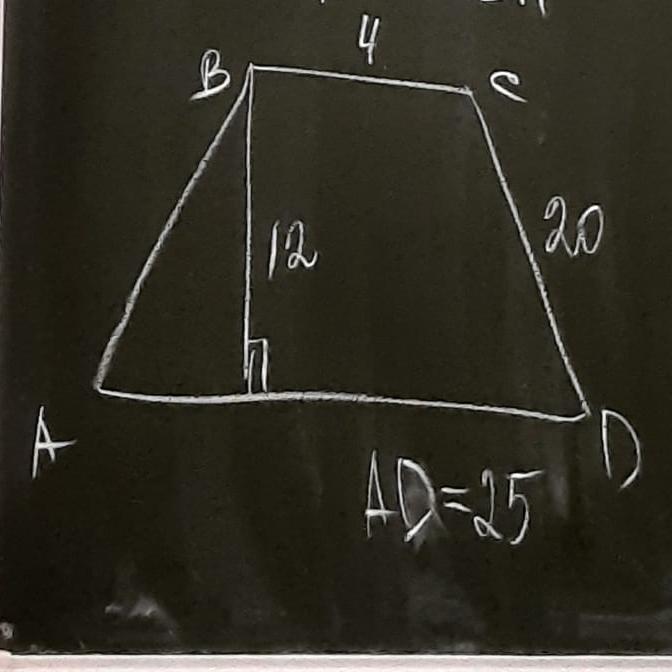Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
Ответ:
Периметр - сумма длин всех сторон
Нам известны почти все стороны, кроме AB
Мы видим, что нам дали высоту Bh= 12 и так же отпустим высоту Ch1 и теперь уже рассматриваем
∆CDh1 - прямоугольный.
по теореме Пифагора найдём h1D:
CD² = h1D² + Ch1²
h1D= √(400-144) = 16
Рассмотрим квадрат BCh1h, у которого все стороны равны => hh1= 4
у нас есть две части основания AD, а именно hh1 = 4 и h1D = 16; найдём третью Ah:
Ah= AD - (hh1 + h1D) = 25 - (4+16) = 25 - 20 = 5
Рассмотрим ∆ABh - прямоугольный
по теореме Пифагора найдём AB:
AB² = Bh² + Ah²
AB= √(144 + 25) = 13
Мы нашли последнюю сторону, которую искали, найдём периметр:
P= 13 + 20 + 25 + 4 = 62
Периметр - сумма длин всех сторон
Нам известны почти все стороны, кроме AB
Мы видим, что нам дали высоту Bh= 12 и так же отпустим высоту Ch1 и теперь уже рассматриваем
∆CDh1 - прямоугольный.
по теореме Пифагора найдём h1D:
CD² = h1D² + Ch1²
h1D= √(400-144) = 16
Рассмотрим квадрат BCh1h, у которого все стороны равны => hh1= 4
у нас есть две части основания AD, а именно hh1 = 4 и h1D = 16; найдём третью Ah:
Ah= AD - (hh1 + h1D) = 25 - (4+16) = 25 - 20 = 5
Рассмотрим ∆ABh - прямоугольный
по теореме Пифагора найдём AB:
AB² = Bh² + Ah²
AB= √(144 + 25) = 13
Мы нашли последнюю сторону, которую искали, найдём периметр:
P= 13 + 20 + 25 + 4 = 62
0
·
Хороший ответ
17 декабря 2022 10:57
Остались вопросы?
Еще вопросы по категории Геометрия
Найдите площадь четырехугольника, изображенного на рисунке. Диагонали четырехугольника перпендикулярны...
диагональ AC прямоугольника ABCD равна 3 см и составляет со стороной AD угол 30 градусов Найдите площадь прямоугольника ABCD...
Найдите углы прямоугольной трапеции если больший из них равен 140 градусов...
Что такое смежный угол? (если можно,с картинкой)...
Как определить по 3 сторонам тип треугольника . Остроугольный, тупоугольный и прямоугольный . Можно ли составить уравнение без теоремы косинусов ?...