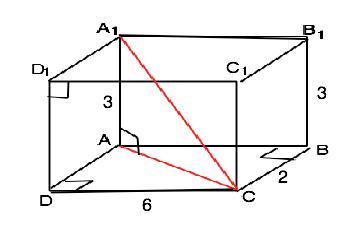
Измерения прямоугольного параллелепипеда равны 2 см, 3 см, 6 см. Найдите его диагональ.

1 ответ

Посмотреть ответы

Megamozg

2205

Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов его измерений:
D²=a²+b²+c² ⇒ D=√(a²+b²+c²)
Объяснение:
Ребра прямоугольного параллелепипеда перпендикулярны основанию, основание – прямоугольник. ⇒ В параллелепипеде АВСDD1A1B1C1 треугольник АА1С - прямоугольный, его гипотенуза СА1 – диагональ параллелепипеда.
СА1²=АА1²+АС². По т.Пифагора находим квадрат диагонали основания: АС²=AB²+BC² =2²+6²= 40 (см) Затем по т.Пифагора – диагональ А1С=√(40+3²)=√49=7(см)

Хороший ответ

17 декабря 2022 19:43

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Отрезок ЕК = 11см не пересекает плоскость, его концы удалены от плоскости на расстоянии 2 см и 7 см. Найти длину проекции отрезка на плоскость... Чему равна площадь равностороннего треугольника,высота которого 9 см?... Дан куб ABCDA1B1C1D1. Докажите ,что плоскости ABC1 и A1B1D перпендикулярны... Основание равнобедренного треугольника равно 18 см, а боковая сторона равна 15 см. Найдите радиус вписанной в треугольник и описанной около треугольни... Ребяяяят 50 баллов В прямоугольном треугольнике DCE с прямым углом С проведена биссектриса EF, причем FC = 13см. Найти расстояние от точки F до прямой...