Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
15 декабря 2022 22:17
607
Помогите решить методом Гаусса( только не через калькулятор)
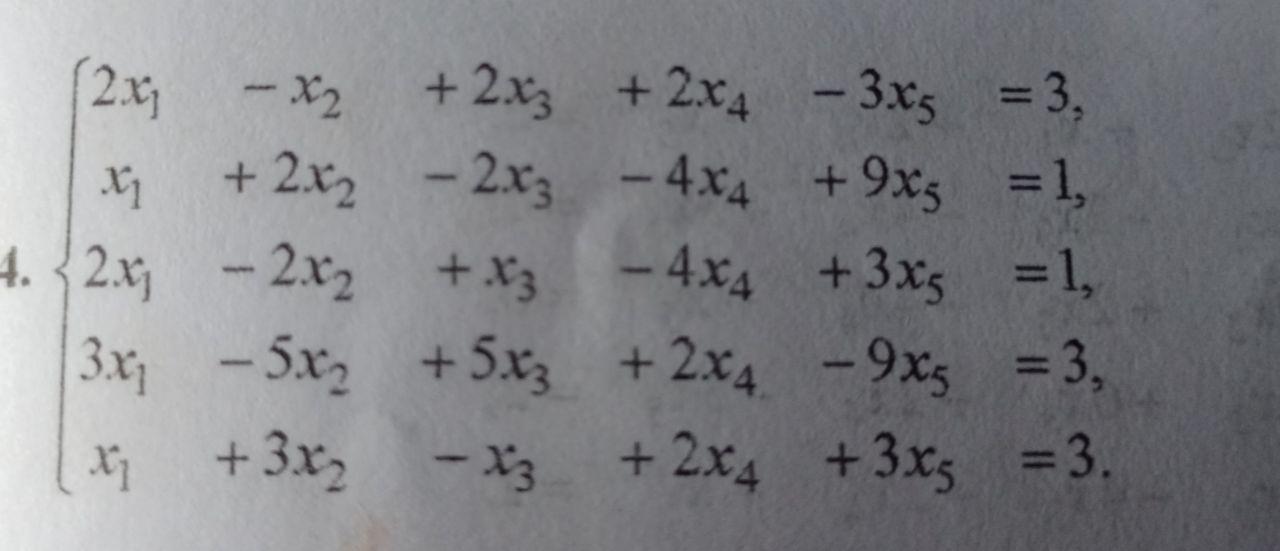
1
ответ
Ответ:
Матричный вид записи: Ax=b, где
A=
2
0
2
2
3
0
2
2
4
9
2
2
0
4
3
3
5
5
2
9
0
3
0
2
3
, b=
3
1
1
3
3
Для решения системы, построим расширенную матрицу:
2
0
2
2
3
3
0
2
2
4
9
1
2
2
0
4
3
1
3
5
5
2
9
3
0
3
0
2
3
3
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a1,1. Для этого сложим строки 3,4 со строкой 1, умноженной на -1,-3/2 соответственно:
2
0
2
2
3
3
0
2
2
4
9
1
0
2
−2
2
0
−2
0
5
2
−1
9
2
−
3
2
0
3
0
2
3
3
Исключим элементы 2-го столбца матрицы ниже элемента a2,2. Для этого сложим строки 3,4,5 со строкой 2, умноженной на -1,-5/2,-3/2 соответственно:
2
0
2
2
3
3
0
2
2
4
9
1
0
0
−4
−2
−9
−3
0
0
−3
−11
−18
−4
0
0
−3
−4
−
21
2
3
2
Исключим элементы 3-го столбца матрицы ниже элемента a3,3. Для этого сложим строки 4,5 со строкой 3, умноженной на -3/4,-3/4 соответственно:
2
0
2
2
3
3
0
2
2
4
9
1
0
0
−4
−2
−9
−3
0
0
0
−
19
2
−
45
4
−
7
4
0
0
0
−
5
2
−
15
4
15
4
Исключим элементы 4-го столбца матрицы ниже элемента a4,4. Для этого сложим строку 5 со строкой 4, умноженной на -5/19:
2
0
2
2
3
3
0
2
2
4
9
1
0
0
−4
−2
−9
−3
0
0
0
−
19
2
−
45
4
−
7
4
0
0
0
0
−
15
19
80
19
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
1
0
1
1
3
2
3
2
0
1
1
2
9
2
1
2
0
0
1
1
2
9
4
3
4
0
0
0
1
45
38
7
38
0
0
0
0
1
−
16
3
Из расширенной матрицы восстановим систему линейных уравнений:
1 x1
+
0 x2
+
1 x3
+
1 x4
+
3
2
x5
=
3
2
0 x1
+
1 x2
+
1 x3
+
2 x4
+
9
2
x5
=
1
2
0 x1
+
0 x2
+
1 x3
+
1
2
x4
+
9
4
x5
=
3
4
0 x1
+
0 x2
+
0 x3
+
1 x4
+
45
38
x5
=
7
38
0 x1
+
0 x2
+
0 x3
+
0 x4
+
1 x5
=
−
16
3
Базисные переменные x1, x2, x3, x4, x5.
Имеем:
x1=
3
2
−1
· x3
−1
· x4
−
3
2
· x5
x2=
1
2
−1
· x3
−2
· x4
−
9
2
· x5
x3=
3
4
−
1
2
· x4
−
9
4
· x5
x4=
7
38
−
45
38
· x5
x5=
−
16
3
Подставив нижние выражения в верхние, получим решение.
x1=
−
13
2
x2=
2
x3=
19
2
x4=
13
2
x5=
−
16
3
Решение в векторном виде:
x=
x1
x2
x3
x4
x5
=
−
13
2
2
19
2
13
2
−
16
3
Матричный вид записи: Ax=b, где
A=
2
0
2
2
3
0
2
2
4
9
2
2
0
4
3
3
5
5
2
9
0
3
0
2
3
, b=
3
1
1
3
3
Для решения системы, построим расширенную матрицу:
2
0
2
2
3
3
0
2
2
4
9
1
2
2
0
4
3
1
3
5
5
2
9
3
0
3
0
2
3
3
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a1,1. Для этого сложим строки 3,4 со строкой 1, умноженной на -1,-3/2 соответственно:
2
0
2
2
3
3
0
2
2
4
9
1
0
2
−2
2
0
−2
0
5
2
−1
9
2
−
3
2
0
3
0
2
3
3
Исключим элементы 2-го столбца матрицы ниже элемента a2,2. Для этого сложим строки 3,4,5 со строкой 2, умноженной на -1,-5/2,-3/2 соответственно:
2
0
2
2
3
3
0
2
2
4
9
1
0
0
−4
−2
−9
−3
0
0
−3
−11
−18
−4
0
0
−3
−4
−
21
2
3
2
Исключим элементы 3-го столбца матрицы ниже элемента a3,3. Для этого сложим строки 4,5 со строкой 3, умноженной на -3/4,-3/4 соответственно:
2
0
2
2
3
3
0
2
2
4
9
1
0
0
−4
−2
−9
−3
0
0
0
−
19
2
−
45
4
−
7
4
0
0
0
−
5
2
−
15
4
15
4
Исключим элементы 4-го столбца матрицы ниже элемента a4,4. Для этого сложим строку 5 со строкой 4, умноженной на -5/19:
2
0
2
2
3
3
0
2
2
4
9
1
0
0
−4
−2
−9
−3
0
0
0
−
19
2
−
45
4
−
7
4
0
0
0
0
−
15
19
80
19
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
1
0
1
1
3
2
3
2
0
1
1
2
9
2
1
2
0
0
1
1
2
9
4
3
4
0
0
0
1
45
38
7
38
0
0
0
0
1
−
16
3
Из расширенной матрицы восстановим систему линейных уравнений:
1 x1
+
0 x2
+
1 x3
+
1 x4
+
3
2
x5
=
3
2
0 x1
+
1 x2
+
1 x3
+
2 x4
+
9
2
x5
=
1
2
0 x1
+
0 x2
+
1 x3
+
1
2
x4
+
9
4
x5
=
3
4
0 x1
+
0 x2
+
0 x3
+
1 x4
+
45
38
x5
=
7
38
0 x1
+
0 x2
+
0 x3
+
0 x4
+
1 x5
=
−
16
3
Базисные переменные x1, x2, x3, x4, x5.
Имеем:
x1=
3
2
−1
· x3
−1
· x4
−
3
2
· x5
x2=
1
2
−1
· x3
−2
· x4
−
9
2
· x5
x3=
3
4
−
1
2
· x4
−
9
4
· x5
x4=
7
38
−
45
38
· x5
x5=
−
16
3
Подставив нижние выражения в верхние, получим решение.
x1=
−
13
2
x2=
2
x3=
19
2
x4=
13
2
x5=
−
16
3
Решение в векторном виде:
x=
x1
x2
x3
x4
x5
=
−
13
2
2
19
2
13
2
−
16
3
0
·
Хороший ответ
17 декабря 2022 22:17
Остались вопросы?
Еще вопросы по категории Математика
Владимир является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором...
В 8 ч.вечера Миша поставил будильник на 9 ч.утра.Через сколько часов зазвонит будильник?...
Груз перевозили в двух контейнерах.В первом контейнере перевезли 5 1/8т груза,а во втором на 2 1/2т меньше.Какова общая масса перевезённого груза?...
Учитель музыки играет одну ноту. Какова вероятность, что эта нота — до? запиши ответ несократимой дробью...
От одной станции одновременно в противоположных направлениях выехали два автобуса. скорость первого автобуса 42 км/ч а скорость второго автобуса 55км/...