Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 895 б
- Dwayne_Johnson 860 б
16 декабря 2022 03:43
1125
Найдите высоту треугольника ABC, опущенную насторону АС, если стороны квадратных клеток равны
√10
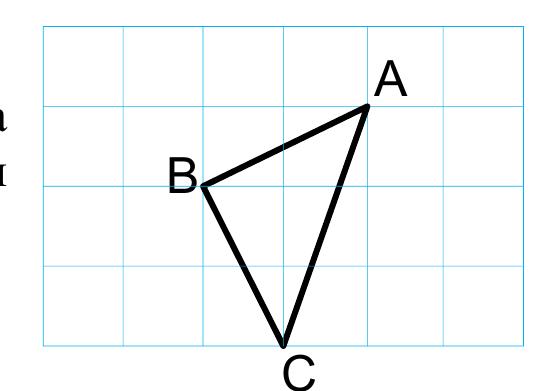
1
ответ
В ΔАВС
АВ² = (√10)²+(2√10)²=50 ⇒ АВ=√50
ВС² = (√10)²+(2√10)²=50 ⇒ АВ=√50
АС² = ( (√10)²+(3√10)²=100 ⇒ АС=10
Высота проведенная к основанию АС делит ΔАВС на два равных прямоугольных треугольника с гипотенузой √50 и катетом 10:2=5
h² = (√50)² - (√25)²=25
h=5
АВ² = (√10)²+(2√10)²=50 ⇒ АВ=√50
ВС² = (√10)²+(2√10)²=50 ⇒ АВ=√50
АС² = ( (√10)²+(3√10)²=100 ⇒ АС=10
Высота проведенная к основанию АС делит ΔАВС на два равных прямоугольных треугольника с гипотенузой √50 и катетом 10:2=5
h² = (√50)² - (√25)²=25
h=5
0
·
Хороший ответ
18 декабря 2022 03:43
Остались вопросы?
Еще вопросы по категории Алгебра
Все предметы 
