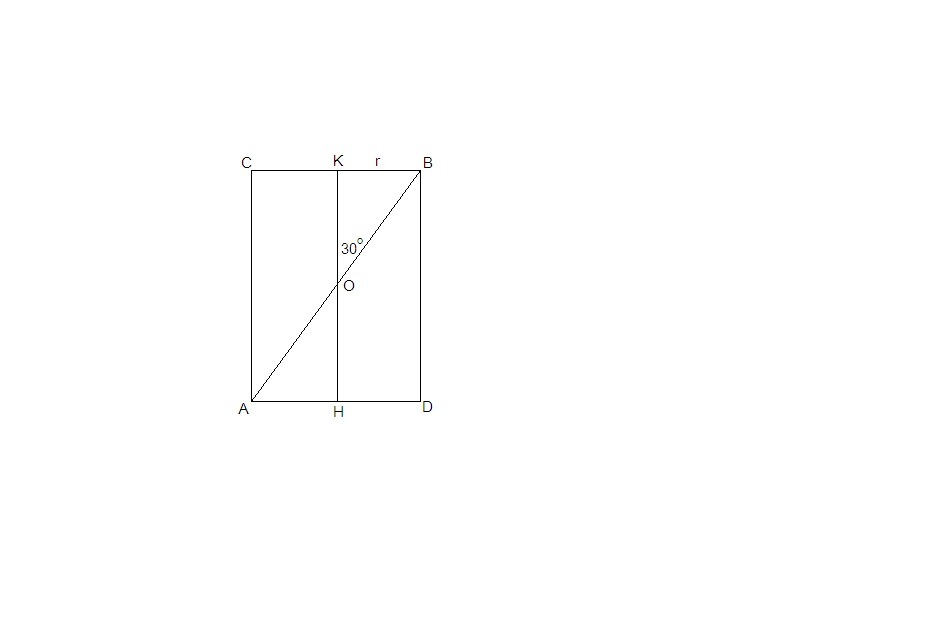
Отрезок АВ, концы которого лежат на арзных окружностях оснований цилиндра, пересекает ось цилиндра под углом 30 градусов. Найти объем цилиндра, если отрезок АВ = 4 корня из 3

1 ответ

Посмотреть ответы

DevAdmin

1720

Т.к. отрезок АВ пересекает ось цилиндра, они лежат в одной плоскости. Осевое сечение цилиндра на рисунке.
ΔКОВ = ΔНОА по катету и прилежащему острому углу (KB = AH = r, ∠КОВ = ∠НОА как вертикальные) ⇒ КО = ОН, АО = ОВ = АВ/2 = 2√3
ΔКОВ:
∠ОКВ = 90°, КВ = ОВ/2 = √3 как катет, лежащий напротив угла в 30°.
r = √3
ОК = ОВ·cos30° = 2√3·√3/2= 3 ⇒ KH = 6
h = 6 высота цилиндра
V = Sосн · h = πr²·h = π · 3 · 6 = 18π

Хороший ответ

19 декабря 2022 05:25

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Начертить угол 120 градусов и провести биссектрису смежного с ним угла... Площадь сечения шара плоскостью равна 16π м2, а площадь параллельного ему сечения, проходящего через центр шара, равна 25π м2. Найдите расстояние межд... В правильной n-угольной призме сторона основания равна а и высота равна h. Вычислите площадь боковой и полной поверхностей призмы, если: а) n = 3, а=1... 1)Высота равнобедренного прямоугольного треугольника, проведенная к гипотенузе, равна 10 см. Найти гипотенузу этого треугольника. 2) В прямоугольном... Как можно найти радиус окружности, описанной около треугольника, если известны сторона треугольника 3см и противоположный ей угол: 1)120° 2)30° 3)135°...