Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
17 декабря 2022 06:14
1054
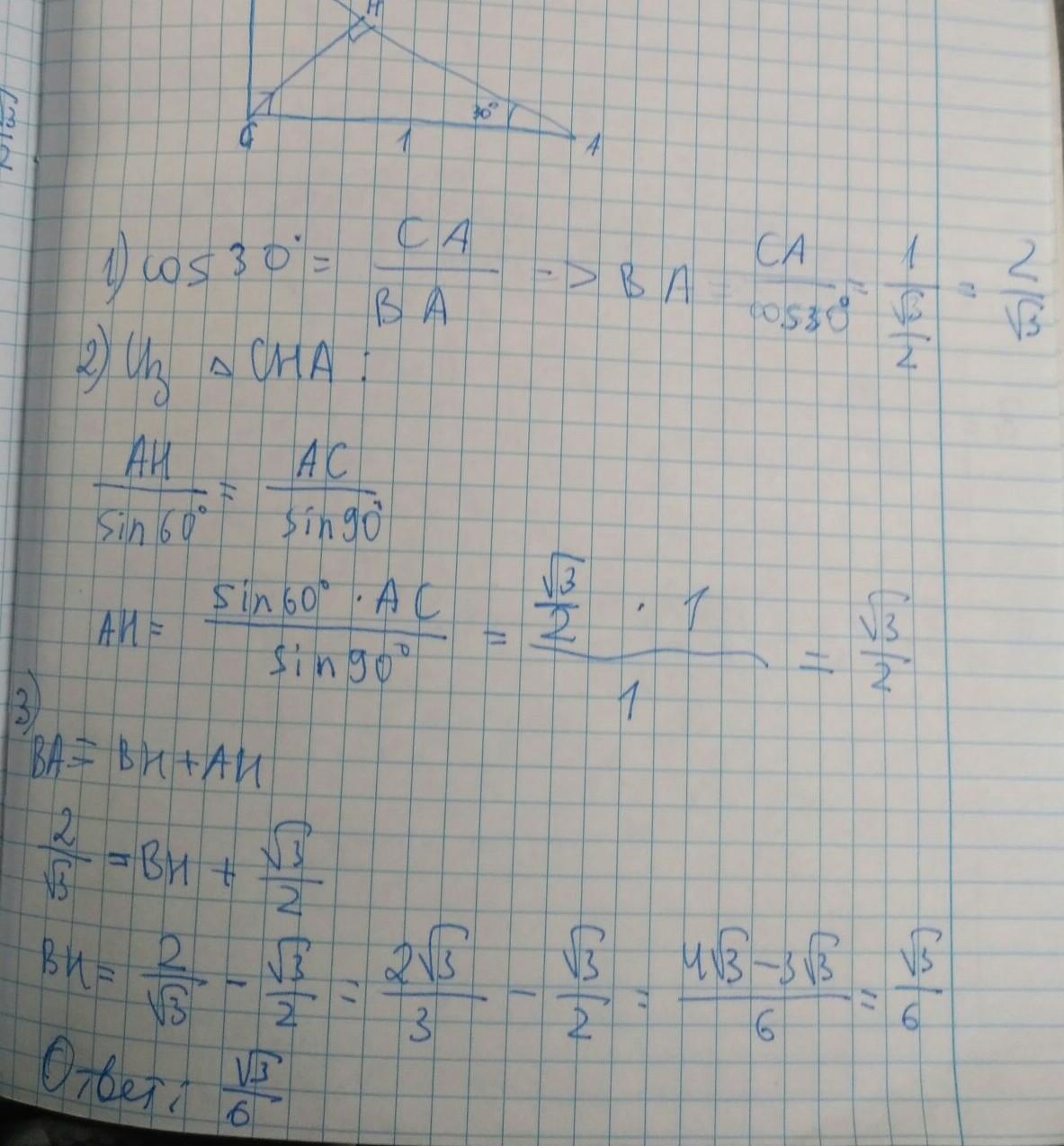
1) В треугольнике ABC угол C равен 90°, CH – высота, угол A равен 30°, AC = 1. Найдите BH.2) В треугольнике ABC угол C равен 90°, CH – высота, угол A равен 30°, BC = 1. Найдите AH.
3) В треугольнике ABC угол C равен 90°, AC=4 sinA=3\5 Найдите высоту CH.
2
ответа
1) в ΔАСН:
СН=0,5 (катет, лежащий против угла в 30° равен половине гипотенузы)
По теореме Пифагора:
АН² = АС² - СН² = 1 - 0,25 = 0,75
АН = √0,75 = 0,5 √3
в ΔАВС:
cos A = AC / AB
AB = 1 ÷ (√3 / 2) = 2√3 / 3
BH = AB - AH = 2√3 / 3 - 0,5√3 = (4√3 - 3√3) / 6 = √3 / 6
Ответ: √3 / 6
2) АВ = 2 ВС = 2 (катет, лежащий против угла в 30° равен половине гипотенузы)
∠В = 180° - ∠С - ∠А = 60°
cos B = BH / BC
BH = 1/2 × 1 = 1/2
AH = AB - BH = 2 - 1/2 = 1 1/2 = 1,5
Ответ: 1,5
3) sin A = CH / AC
CH = sin A × AC = 3/5 × 4 = 12/5 = 2,4
Ответ: 2,4
СН=0,5 (катет, лежащий против угла в 30° равен половине гипотенузы)
По теореме Пифагора:
АН² = АС² - СН² = 1 - 0,25 = 0,75
АН = √0,75 = 0,5 √3
в ΔАВС:
cos A = AC / AB
AB = 1 ÷ (√3 / 2) = 2√3 / 3
BH = AB - AH = 2√3 / 3 - 0,5√3 = (4√3 - 3√3) / 6 = √3 / 6
Ответ: √3 / 6
2) АВ = 2 ВС = 2 (катет, лежащий против угла в 30° равен половине гипотенузы)
∠В = 180° - ∠С - ∠А = 60°
cos B = BH / BC
BH = 1/2 × 1 = 1/2
AH = AB - BH = 2 - 1/2 = 1 1/2 = 1,5
Ответ: 1,5
3) sin A = CH / AC
CH = sin A × AC = 3/5 × 4 = 12/5 = 2,4
Ответ: 2,4
0
·
Хороший ответ
19 декабря 2022 06:14
Решение в приложении. 1 фотка-1 номер; 2 фотка- 2 номер; 3 фотка- 3 номер.
0
19 декабря 2022 06:14
Остались вопросы?
Еще вопросы по категории Геометрия
К окружности с центром О проведена касательная FK(K-точка касания).Найдите отрезок FK, если радиус окружности равен 14 см и угол FOK=45 градусов. С РИ...
Помогите пожалуйста с геометрией...
Зависит ли величина площади фигуры от того, по какой формуле площади она вычисляется? Если нет то почему ?...
Центральный угол AOB равен 60. опирается на хорду AB длиной 4. найдите радиус окружности....
Пожалуйста,срочно!!! Дана правильная четырехугольная призма, C1K перпендикулярна D1C, C1K=24 см, KC=32 см.Найти площадь полной поверхности призмы.Долж...