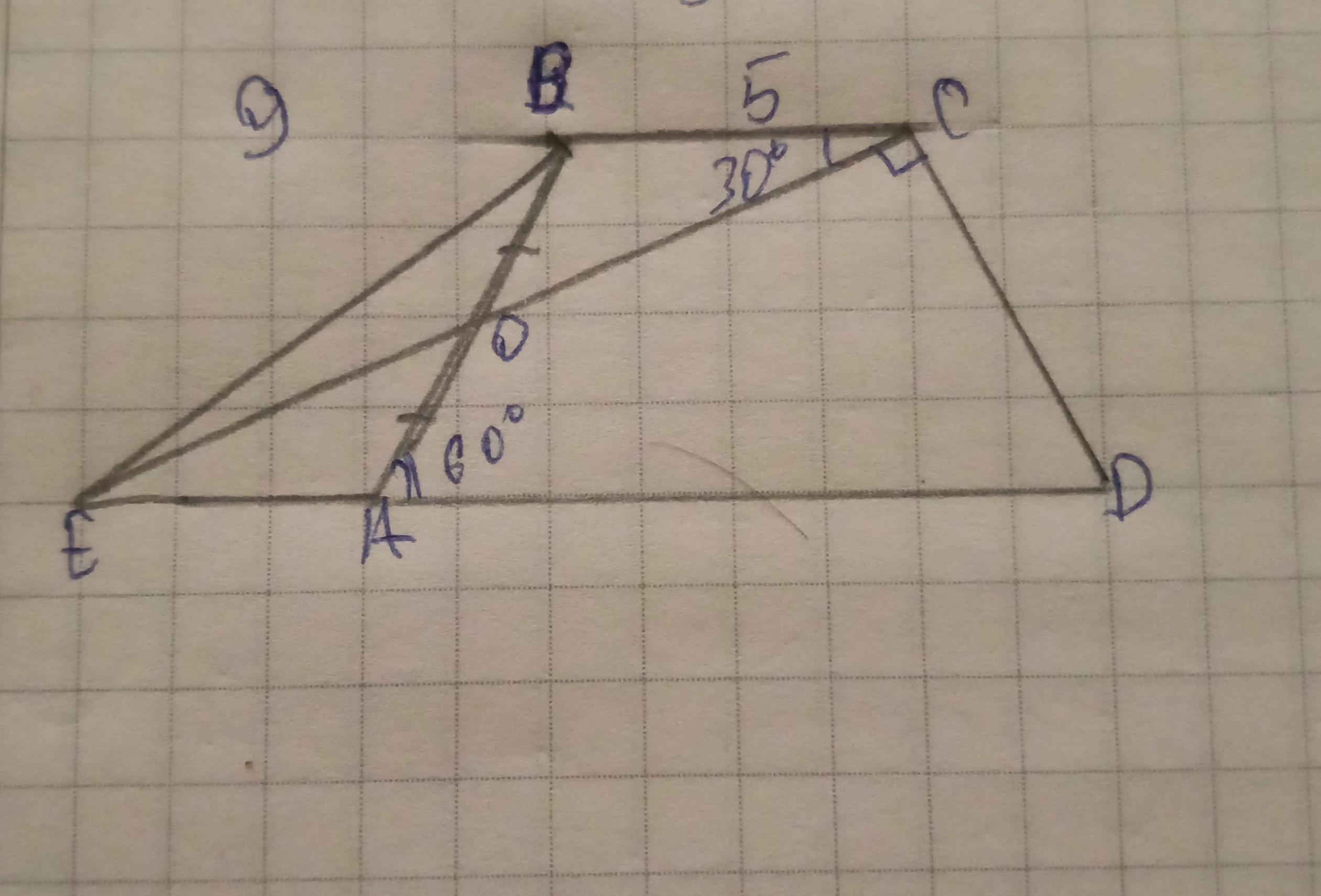
Найти периметр трапеции ABCD,если известно, что AD=15

Ответ:
Периметр трапеции ABCD равен 40 ед.
Объяснение:
Найти периметр трапеции ABCD,если известно, что ВС=5, AD=15, ∠ВАD = 60°. Через середину боковой стороны АВ проведена прямая ЕС так, что ∠ВСЕ=30°, а ∠ЕСD=90°.
Периметр трапеции - это сумма всех её сторон.
Р(ABCD) = АВ+ВС+СD+AD.
Так как стороны ВС и AD. нам известны, задача сводится к нахождению боковых сторон AB и CD.

1) ∠ВСD = ∠ВСЕ+∠ЕСD = 30°+90° = 120°
Так как сумма углов, прилежащих к боковой стороне, равна 180 °, то:
∠АDC = 180°-∠ВСD=180°-120°=60°.

• Если у трапеции углы при основании равны, то она - равнобедренная.

Так как ∠ВАD = ∠АDC = 60°, то ABCD - равнобедренная трапеция.

2)Рассмотрим ΔОАЕ и ΔОВС.
АО=ОВ - по условию, ∠АОЕ=∠ВОС - как вертикальные, ∠ЕАО=∠СВО - как внутренние накрест лежащие углы при параллельных прямых ВС и ЕD и секущей АВ.
Следовательно ΔОАЕ = ΔОВС по стороне и двум прилежащим к ней углам ( ІІ признак равенства треугольников).
Из равенства треугольников следует равенство соответствующих сторон:
ЕА=ВС= 5 ед
Значит ЕD = EA+AD = 5+15 = 20 ед

3) ∠СЕD = ∠ВСЕ = 30° - как внутренние накрест лежащие углы при параллельных прямых ВС и ЕD и секущей ЕС.
Рассмотрим прямоугольный ΔЕСD (∠ЕСD=90°)

• Катет, лежащий напротив угла в 30° равен половине гипотенузы.

Поэтому CD = 1/2 * ЕD = 1/2 * 20 = 10 ед.

4) Так как ABCD - равнобедренная трапеция, то у неё боковые стороны равны:
АВ = CD = 10 ед.

5) Р(ABCD) = АВ+ВС+СD+AD = 10+5+10+15= 40 ед
#SPJ3