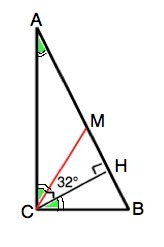
В прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла, равен 32 градуса. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах

1 ответ

Посмотреть ответы

DevAdmin

1720

Медиана прямоугольного треугольника, проведенная из прямого угла, равна половине гипотенузы и делит треугольник на два равнобедренных.
В ∆ АМС ∠САМ=∠МАС,
Высота, проведенная из прямого угла, делит прямоугольный треугольник на подобные. ⇒∠НСВ=∠НАС=МАС.
∠АСВ=угол АСМ+угол МСН+угол НСВ.
Так как углы САМ и НСВ равны, то
2 ∠САМ+32°=90°
∠САМ=(90°-32°):2=58°:2=29°
Сумма острых углов прямоугольного треугольника равна 90° ⇒
∠АВС=90°-29°=61°

Хороший ответ

28 декабря 2022 01:11

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Решить треугольник АВС,если <в=30 гр.,<с=105 гр.,вс=3 корня из 2 см :)... Большая боковая сторона прямоугольной трапеции равна 12√2см, а острый угол - 45°. Найдите площадь трапеции, если известно, что в нее можно ВПИСАТЬ окр... 40 баллов дам!!! Пжж Напишите: 1.Определение параллелограмма.Свойства параллелограмма,доказательство любого свойства. 2.Определение параллелограмм... Высота правильной треугольной пирамиды равна 8 см. Радиус окружности, описанной около ее основания-8 корней из 3. Вычислить: а) длину бокового ребра п... В правильной четырехугольной пирамиде сторона основания равна 12, а длина бокового ребра равна 11. Найдите высоту пирамиды....