Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
26 декабря 2022 02:27
613
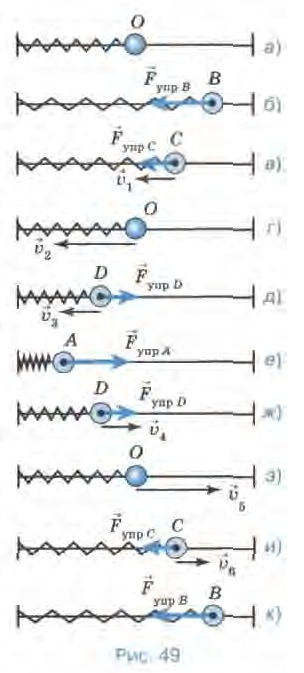
Горизонтальный пружинный маятник, изображенный на рисунке, совершает свободные колебания. Какие величины, характеризующие это движение (амплитуда, частота, период, скорость, сила, под действием которой совершаются колебания), являются постоянными, а какие — переменными? (Трение не учитывайте.
1
ответ
Раз трение отсутствует, то колебания являются незатухающими, то есть, амплитуда (максимальное отклонение от положения равновесия) неизменна.
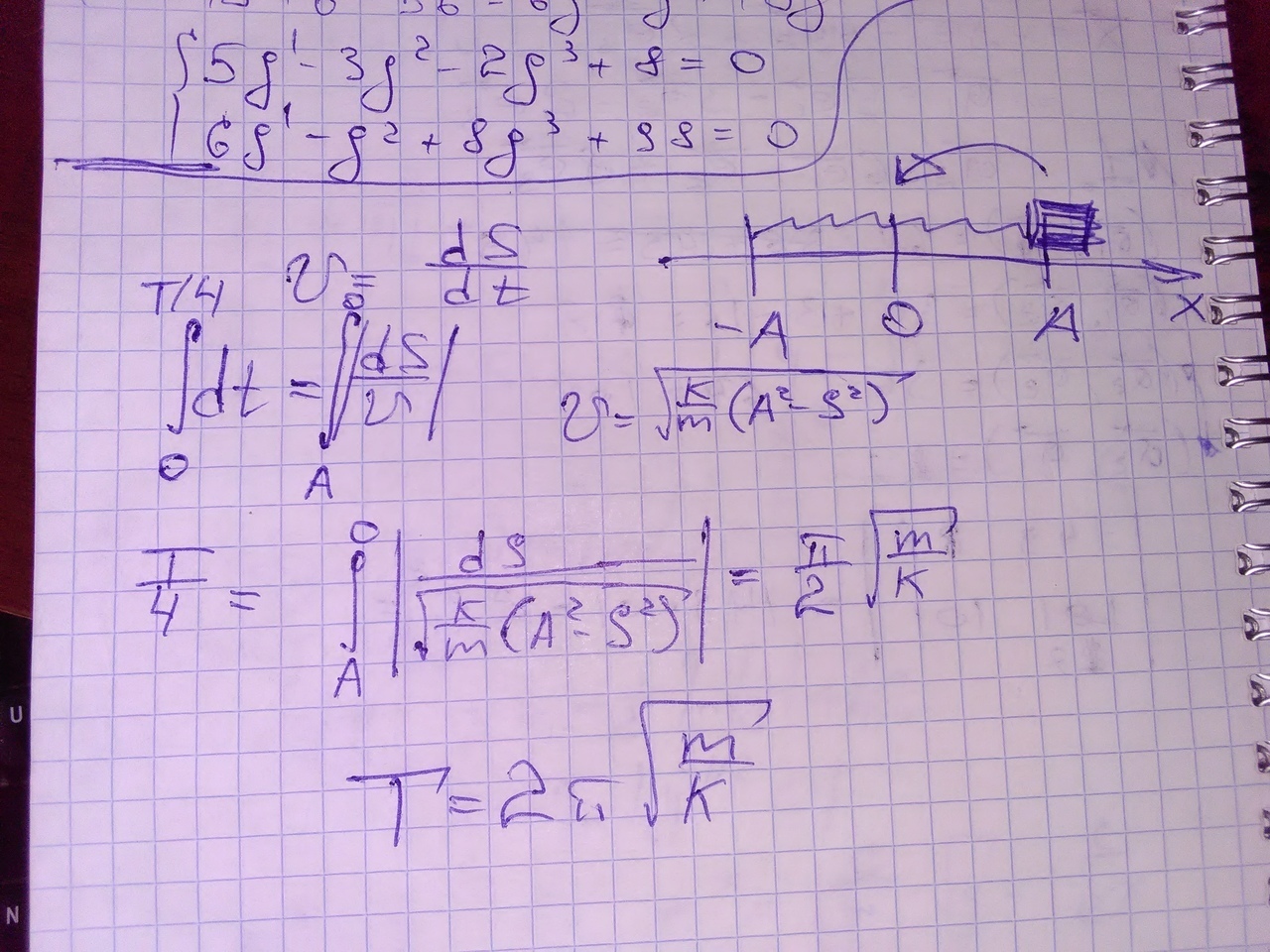
Период колебаний пружинного маятника, как известно, равен:
T = 2π √[m/k].
Так как масса груза и жесткость пружины есть величины постоянные, то период колебаний неизменен. Следовательно, неизменна и частота колебаний (v = 1/T).
Сила, под действием которой совершаются колебания, - это сила упругости. Она, согласно закону Гука, равна Fупр = k Δx, где Δx - деформация пружины. Величина Δx, разумеется, в ходе колебаний изменяется, а, следовательно, изменяется и сила.
Напишем закон сохранения энергии для колеблющегося тела:
(k A²)/2 = (m v²)/2 + (k Δx²)/2 - максимальная потенциальная энергия деформированной пружины переходит в кинетическую энергию груза и также в потенциальную энергию деформированной пружины.
Нетрудно сообразить, что из этого уравнения следует, что скорость является также переменной величиной и зависит от величины деформации пружины.
кстати, не сразу вспомнил про формулу периода пружинного маятника, и потому ринулся в "чуть" не ту сторону, из-за чего в конечном счете случайно вывел эту самую формулу. забавно, в общем, получилось. краткую версию моего вывода прикрепляю
Период колебаний пружинного маятника, как известно, равен:
T = 2π √[m/k].
Так как масса груза и жесткость пружины есть величины постоянные, то период колебаний неизменен. Следовательно, неизменна и частота колебаний (v = 1/T).
Сила, под действием которой совершаются колебания, - это сила упругости. Она, согласно закону Гука, равна Fупр = k Δx, где Δx - деформация пружины. Величина Δx, разумеется, в ходе колебаний изменяется, а, следовательно, изменяется и сила.
Напишем закон сохранения энергии для колеблющегося тела:
(k A²)/2 = (m v²)/2 + (k Δx²)/2 - максимальная потенциальная энергия деформированной пружины переходит в кинетическую энергию груза и также в потенциальную энергию деформированной пружины.
Нетрудно сообразить, что из этого уравнения следует, что скорость является также переменной величиной и зависит от величины деформации пружины.
кстати, не сразу вспомнил про формулу периода пружинного маятника, и потому ринулся в "чуть" не ту сторону, из-за чего в конечном счете случайно вывел эту самую формулу. забавно, в общем, получилось. краткую версию моего вывода прикрепляю
0
·
Хороший ответ
28 декабря 2022 02:27
Остались вопросы?
Еще вопросы по категории Физика
Что такой A (физика )...
Шар катится по горизонтальной поверхности и останавливается, при этом... ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ: А. Кинетическая энергия Б. Потенциальная энергия ИЗМЕНЕН...
мальчик массой 20 кг стоя на коньках горизонтально бросает камень со скоростью 5 м/с. Чему равна горизонтальная скорость мальчика, если масса камня 1...
Как расположены частицы в твёрдых телах?...
1)Напряжение на концах проводника 0,2кВ, а сила тока в нём 10А.Какого сопротивление противодника?...