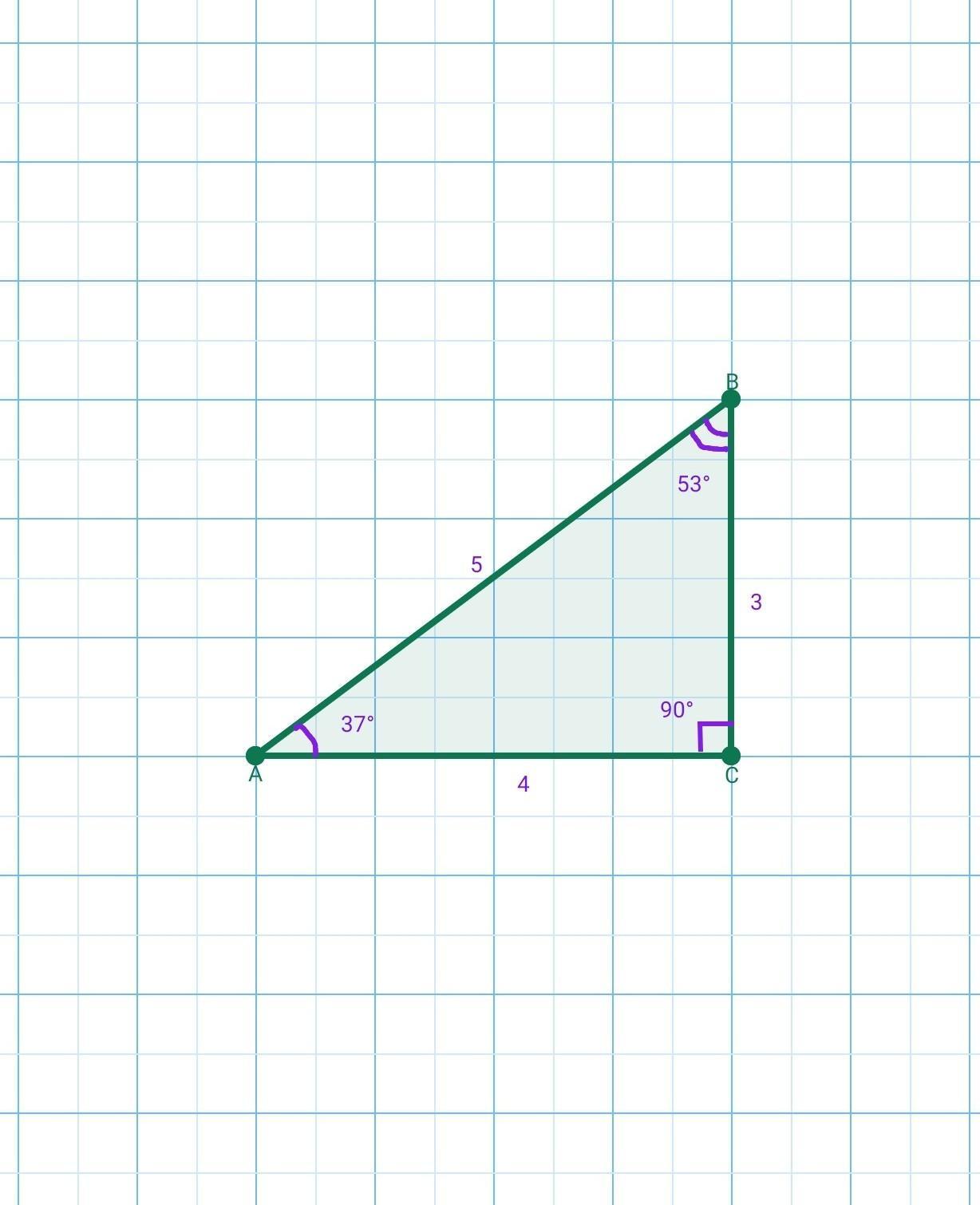
Чему равны углы прямоугольного треугольника со сторонами 3 4 5

1 ответ

Посмотреть ответы

Megamozg

2205

Ответ:
Углы прямоугольного треугольника со сторонами 3, 4 и 5 равны:
∠С=90°, ∠А≈37°, ∠В≈53°.
Объяснение:
Дан прямоугольный треугольник АBC со сторонами: 3, 4, 5. Требуется найти его углы.

Прямоугольным называется треугольник, в котором один угол прямой, то есть равен 90°.
Противоположная прямому углу сторона называется гипотенузой.

Это самая длинная сторона прямоугольного треугольника. Таким образом АВ=5 ед - как гипотенуза прямоугольного треугольника АВС. Следовательно ∠С=90°.
Следовательно АС=4 ед и ВС=3 ед - катеты △ABC.

Найдём ∠А.

Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе.

$\bf cos\angle A = \dfrac = \dfrac = 0,8$
По таблице косинусов находим, что косинус 0,8 примерно соответствует углу 37°:
$\bf \angle A \approx 37^\circ$
Так как сумма острых углов в прямоугольном треугольнике равна 90°, то находим угол В:
$\bf \angle B = 90^\circ - \angle A \approx 90^\circ - 37^\circ \approx 53^\circ$
#SPJ5

Хороший ответ

28 декабря 2022 03:09

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

В △ABC высоты пересекаются в точке H, а биссектрисы в точке Q, ∠AQC=100°. Определи градусную меру угла AHC.... Боковые стороны прямоугольной трапеции равны 15 см и 17 см, средняя линия равна 6 см. Найти основание трапеции.... Треугольник АВС- прямоугольный и равнобедренный с прямым углом С и гипотенузой 10 см. Отрезок СМ перпендикулярен плоскости треугольника. Расстояние о... Найдите тангенс <С ∆ ABC, изображённого на рисунке.... Найдите площадь правильного многоугольника, если площадь его незакрашенной части равна 70см²....

Чему равны углы прямоугольного треугольника со сторонами 3 4 5​

Чему равны углы прямоугольного треугольника со сторонами 3 4 5