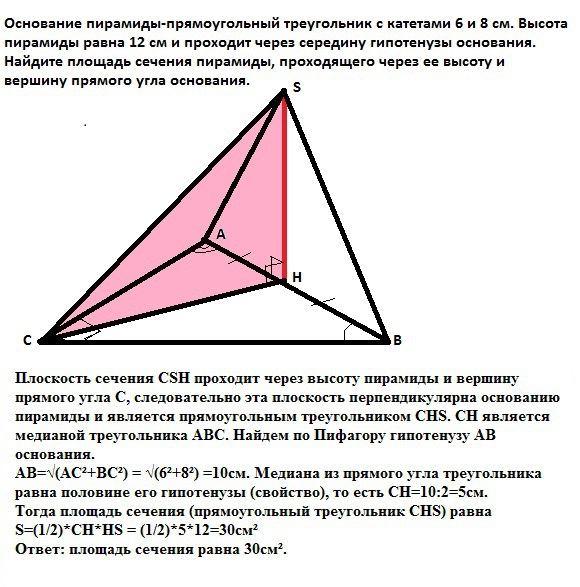
Основание пирамиды-прямоугольный треугольник с катетами 6 и 8 см. Высота пирамиды равна 12 см и проходит через середину гипотенузы основания. Найдите площадь сечения пирамиды, проходящего через ее высоту и вершину прямого угла основания.

1 ответ

Посмотреть ответы

DevAdmin

1720

Плоскость сечения СSH проходит через высоту пирамиды и вершину прямого угла С, следовательно эта плоскость перпендикулярна основанию пирамиды и является прямоугольным треугольником СНS. СН является медианой треугольника АВС. Найдем по Пифагору гипотенузу АВ основания.
AB=√(АС²+ВС²) = √(6²+8²) =10см. Медиана из прямого угла треугольника равна половине его гипотенузы (свойство), то есть СН=10:2=5см.
Тогда площадь сечения (прямоугольный треугольник СНS) равна
S=(1/2)*СН*НS = (1/2)*5*12=30см²
Ответ: площадь сечения равна 30см².

Хороший ответ

28 декабря 2022 04:03

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Найдите площадь четырехугольника, изображенного на рисунке. Диагонали четырехугольника перпендикулярны... Обчислить: 1) 4 cos 90° + 2 cos 180° - tg 180°; 2) cos 0° - cos 180° + sin 90°.... Какие прямые называются параллельными ???... на боковых сторонах равнобедренного треугольника АВС отложены равные отрезки АМ и АК. Докажите, что ВСМ=СВК... Найдите площадь трапеции, изображенной на рисунке....