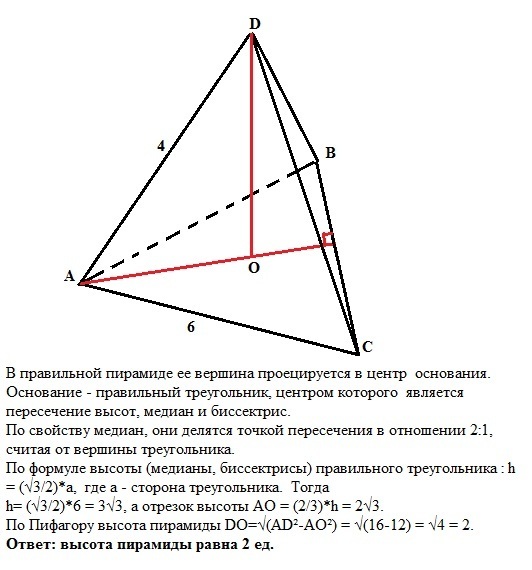
В правильной треугольной пирамиде сторона основания равна 6, а длина бокового ребра равна 4. Найдите высоту пирамиды

1 ответ

Посмотреть ответы

DevAdmin

1720

В правильной пирамиде ее вершина проецируется в центр основания. Основание - правильный треугольник, центром которого является пересечение высот, медиан и биссектрис. По свойству медиан, они делятся точкой пересечения в отношении 2:1, считая от вершины треугольника. По формуле высоты (медианы, биссектрисы) правильного треугольника: h = (√3/2)*a, где а - сторона треугольника. Тогда h=(3/2)*6 = 3√3, а отрезок высоты АО = (2/3)*h = 2√3. По Пифагору высота пирамиды DO=√(AD²-AO²) = √(16-12) = √4 = 2.
Ответ: высота пирамиды равна 2 ед.

Хороший ответ

28 декабря 2022 15:01

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

В равнобедренном треугольнике АВС с основанием АС проведена биссектриса AD.Найдите углы этого треугольника,если АDB =110 решите пожалуйста,срочно!... 1 Точка касания двух окружностей равноудалёна от центров этих окружностей. 2 В параллелограмме есть два равных угла . 3 Площадь прямоугольного треуго... Сторона ромба равна 4, а расстояние от точки пересечения диагоналей ромба до неё равно 1.Найдите площадь. Пожалуйста формулу не забудьте.... в прямоугольном треугольнике ABC угол С= 90 градусов,угол А=30 градусов, ВС= 12 в квадратном корне 2.Найдите гипотенузу Срочно,заранее спасибо... Сформулируйте и докажите теорему о перпендикуляре проведенном из данной точки к данной прямой...