Свойство медиан треугольника (+Доказательство)
8 класс

Ответ:
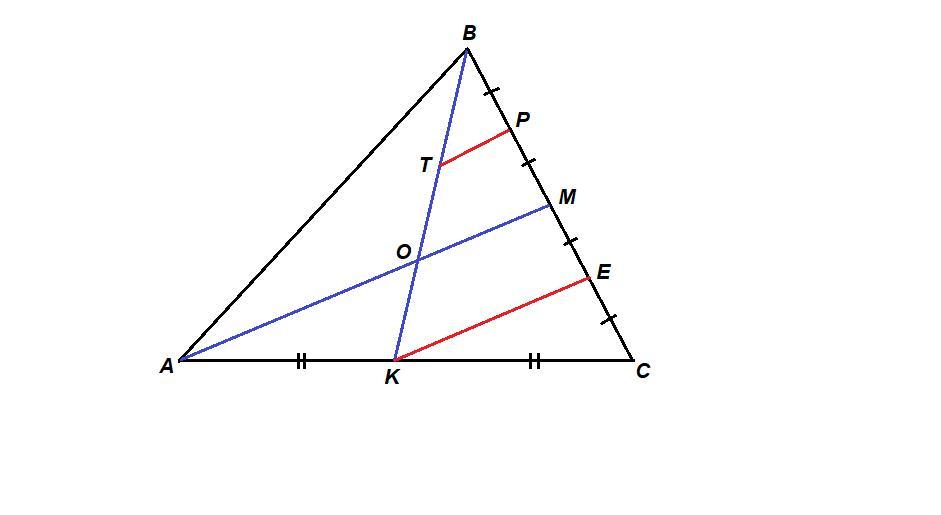
Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2 : 1, считая от вершины.
1) Докажем, что две медианы делятся точкой пересечения в отношении 2 : 1, считая от вершины.
В ΔАВС АМ и ВК - медианы. О - точка пересечения медиан.
Проведем КЕ ║ АМ. Так как АК = КС, то и МЕ = ЕС по теореме Фалеса.
Т.е. Е - середина отрезка МС.
Отметим Р - середину отрезка ВМ и проведем РТ ║ АМ, тогда ВТ = ТО по теореме Фалеса.
Итак, ВР = РМ = МЕ, РТ ║ МО ║ ЕК, значит ВТ = ТО = ОК по теореме Фалеса.
ВО : ОК = 2 : 1.
Аналогично можно доказать, что АО : ОМ = 2 : 1.
2) Докажем, что все три медианы пересекаются в одной точке.
Так как две медианы точкой пересечения делятся 2 : 1, то медиана проведенная из вершины С, должна разделить медиану ВК в отношении 2 : 1, т.е. должна пройти через точку О. Следовательно, все три медианы пересекаются в одной точке.