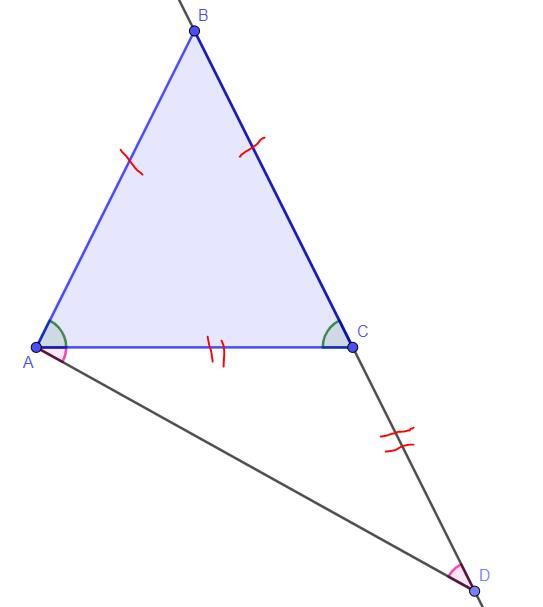
на продолжении стороны BC равнобедренного треугольника ABC с основанием AC отметили точку D так, что CD=AC, точка C находится между точками B и D. Найдите велечину угла ADC, если угол ABC равен 36°. Ответ дайте в градусах. Ответьте!!!! СРОЧНО!!!!!

1 ответ

Посмотреть ответы

DevAdmin

1705

Ответ:

∠ADC = 36°

Объяснение:
Дано: AB = BC, CD = AC, ∠ABC = 36°
Найти: ∠ADC - ?
Решение:
По свойствам равнобедренного треугольника его углы при основании равны, тогда так как треугольник ΔACD и ΔABC - равнобедренные (по условию CD = AC, AB = BC), то угол
∠CAD = ∠CDA и угол ∠BAC = ∠ACB.
По теореме про сумму углов треугольника (ΔABC):
∠BAC + ∠ACB + ∠ABC = 180° ⇒
⇒ $\angle BAC = \angle ACB = \dfrac - \angle ABC} = \dfrac - 36^{\circ}} = \dfrac} = 72^{\circ}$ .
По теореме в треугольнике внешний угол равен сумму двух углов не смежных с ним, тогда угол ∠ACD = ∠ABC + ∠BAC = 36° + 72° = 108°
По теореме про сумму углов треугольника (ΔACD):
∠DAC + ∠CDA + ∠ACD = 180° ⇒
⇒ $\angle CAD = \angle ADC= \dfrac - \angle ACD} = \dfrac - 108^{\circ}} = \dfrac} = 36^{\circ}$ .

Хороший ответ

29 декабря 2022 11:44

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Про углы треугольника 𝐴𝐵𝑂, образованного хордой 𝐴𝐵 и двумя радиусами окружности с центром в точке 𝑂 и радиусом 10, известно, что они относятся к... биссектриса угла прямоугольника делит большую сторону пополам.Меньшая сторона прямоугольника равна 5см. Найдите периметр прямоугольника.... Диаметр шара равен 4m. Черезконец деаметра проведена плоскость под углом 30 градусов к нему. Найдите площадь сечения шара этой плоскастью... Найдите площадь кругового сектора, если градусная мера его дуги равна 120 градусам, а радиус круга равен 12см... Центральные и вписанные углы. Теорема о свойстве вписанного угла....