Докажите что радиус окружности вписанной в прямоугольный Прямоугольный треугольник с катетами А и b гипотенузой C вычисляется по формуле r равно a+b-c:2

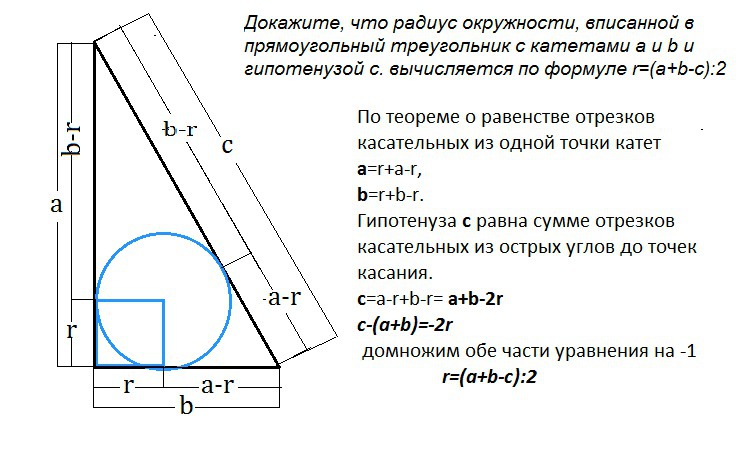
Докажите, что радиус окружности, вписанной в прямоугольный треугольник с катетами а и b и гипотенузой с. вычисляется по формуле r=(a+b-c):2
--------
Вписанная окружность делит стороны треугольника на отрезки, равные от вершины до точек касания.
Отрезки касательных, проведенных из одной точки к окружности, равны.
Если катеты равны a и b, то расстояние от вершины угла до точки касания равно:
на катете а =a-r,
на катете b=b-r.
Гипотенуза с равна сумме отрезков касательных из острых углов до точек касания.
с=a-r+b-r= a+b-2r
c-(a+b)=-2r домножим обе части уравнения на -1
r=(a+b-c):2, что и требовалось доказать.