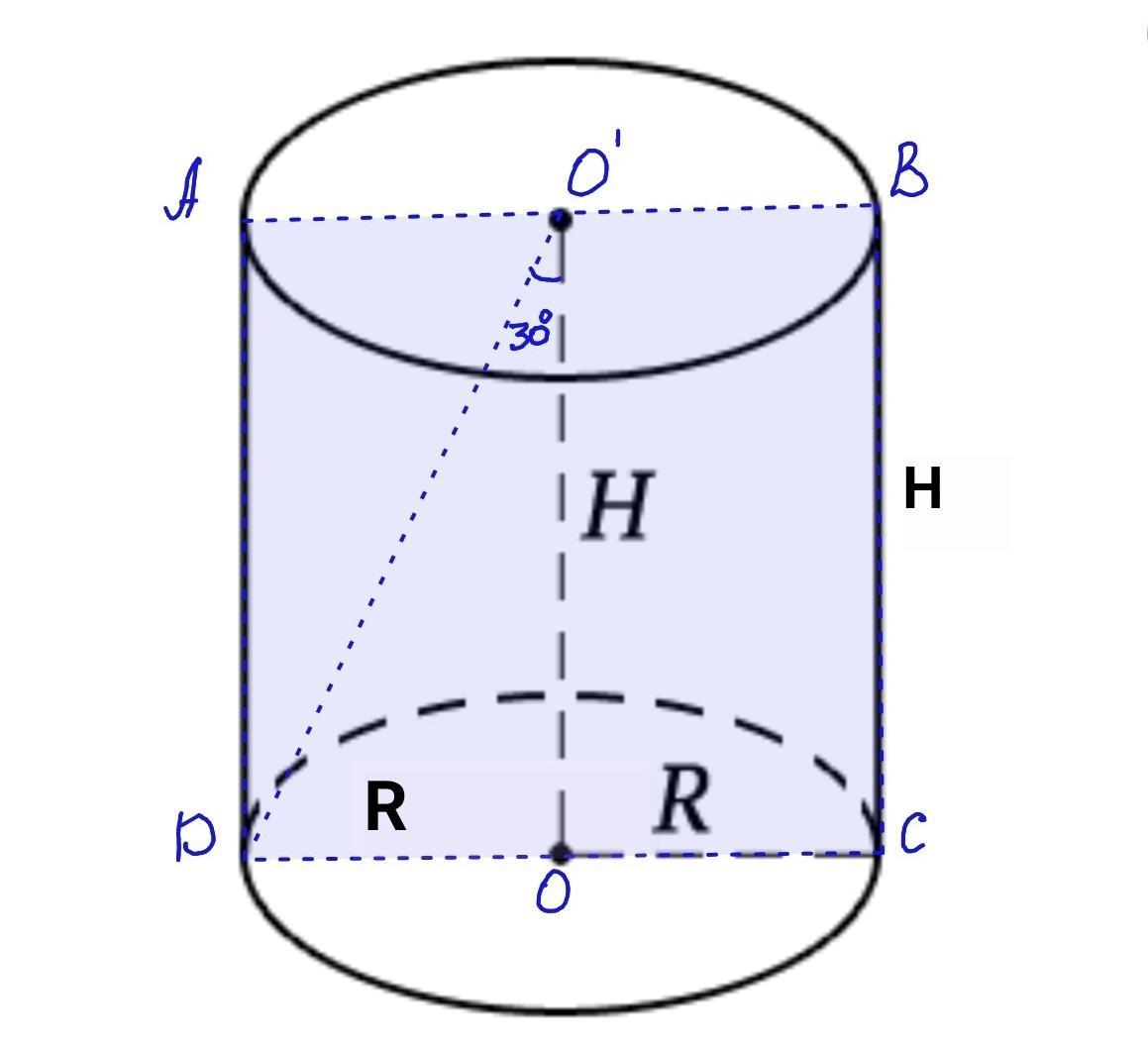
Площадь осевого сечения цилиндра равна 18√3 см2. Отрезок, соединяющий центр верхнего основания цилиндра с точкой окружности нижнего основания образует с осью цилиндра угол 30°. Найдите площадь боковой поверхности цилиндра.С чертежом...
ДАЮ 50 БАЛЛОВ ​

Ответ:
Площадь боковой поверхности цилиндра 18π√3 см²
Объяснение:
Площадь осевого сечения цилиндра равна 18√3 см². Отрезок, соединяющий центр верхнего основания цилиндра с точкой окружности нижнего основания образует с осью цилиндра угол 30°. Найдите площадь боковой поверхности цилиндра.

• Осевое сечение цилиндра - это сечение цилиндра плоскостью, которая проходит через ось цилиндра.
• Это сечение является прямоугольником.
• Площадь боковой поверхности цилиндра равна произведению высоты цилиндра на длину окружности основания. S=H•L
• Длина окружности основания L=2πR, R - радиус основания цилиндра.

Решение

Осевое сечение цилиндра - прямоугольник ABCD.
Площадь прямоугольника равна произведению его длины на ширину.

S(ABCD)=BC•DC.

BC - это высота цилиндра (Н), DC - его диаметр.
Известно, что диаметр равен двум радиусам (R): DC=2R.
По условию задачи площадь осевого сечения равна 18√3 см², поэтому наша формула примет вид:
H•2R=18√3 или 2RH=18√3.

Площадь боковой поверхности цилиндра находим по формуле:

S=2πRH,

но 2RH=18√3, поэтому:
S = 18√3•π = 18π√3 см²

#SPJ3