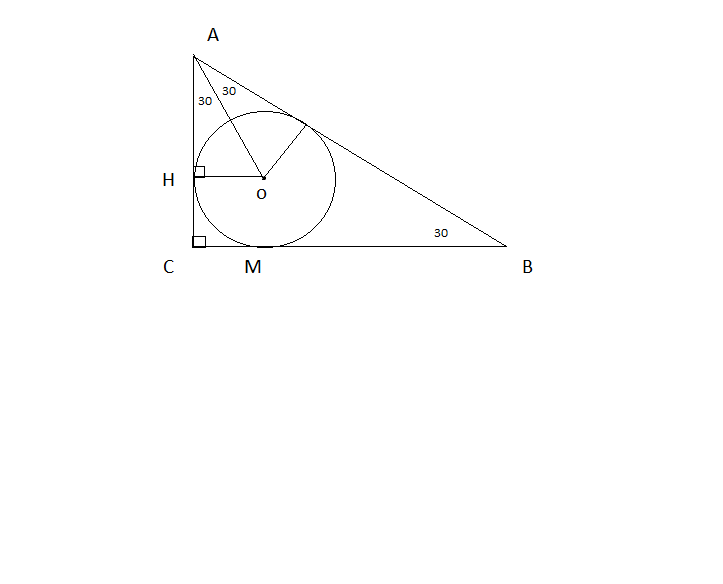
Радиус вписанной в прямоугольный треугольник окружности 3 см О-цунтр вписанной окружност уголь С=90 градусов уголь BAO=30 градусов .Найти площадь треугольника

1 ответ

Посмотреть ответы

DevAdmin

1720

Центр вписанной окружности - точка пересечения биссектрис, следовательно АО - биссектриса <A=60. В прямоугольном треугольнике HOA, катет против угла в 30 градусов равен половине гипотенузе, следовательно АО=6 см. По теореме Пифагора:
$AH^2=AO^2-HO^2=36-9=27\\
AH= \sqrt =3 \sqrt \\\\
AC=CH+AH=3+3 \sqrt\\$
<B=90-<A=30
В прямоугольном треугольнике ABC, катет против угла в 30 градусов равен половине гипотенузе, следовательно АB= $6+6 \sqrt$ см. По теореме Пифагора:
$CB^2=AB^2-CA^2=(6+6 \sqrt)^2-(3+3 \sqrt)^2=108+54 \sqrt\\
CB=3 \sqrt) } \\\\
S=pr= \frac CA*CB
$
Подставляем и считаем

Хороший ответ

16 января 2023 22:53

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

равнобедренный треугольник вписан в окружность, угол при вершине опирается на дугу описанной окружности в 200, найдите все углы треугольника... Дано: NM параллельно AC AM=6см BM=8см AC=21 см а) доказать, что произведение Ab*Bn=CB*BM б) найти MN рисунок во вложенном файле... Сторона ромба равна 4, а расстояние от точки пересечения диагоналей ромба до неё равно 1.Найдите площадь. Пожалуйста формулу не забудьте.... из точки к прямой проведены две наклонные,длины которых 13 см,и 15 см.Найти расстояние от точки до прямой,если разность проэкций наклонных на эту прям... В квадрате каждая вершина соединена с серединой стороны, которая лежит между двумя следующими вершинами (считать вершины в одинаковом порядке). Соедин...