Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
14 января 2023 23:21
919
Помогите решить:
-2sin(7п\2+x)sinx=√3cosx
(2 пример на фото)
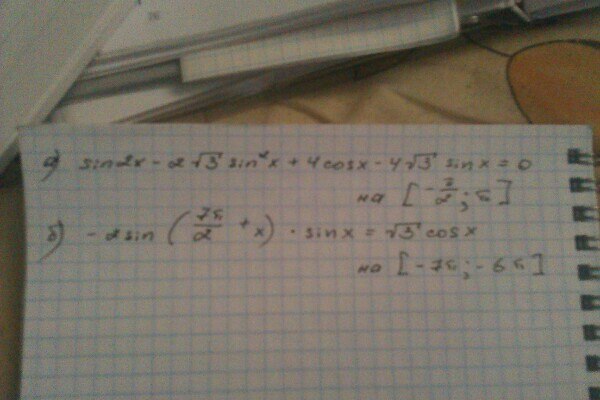
1
ответ
Sin2x-2√3sin²x+4cosx-4√3sinx=0
(2sinxcosx+4cosx)-(2√3sin²x+4√3sinx)=0
2cosx(sinx+2)=2√3sinx(sinx+2)=0
2(sinx+2)(cosx-√3sinx)=0
sinx+2=0 или cosx-√3sinx=0 |:cosx≠0
sinx≠2, т.к. 1-√3tgx=0
|sinx|≤1, a 2>1 tgx=√3/3
x=π/6+πn, n∈Z
[-π/2;π]
x=π/6
Ответ: π/6
-2sin(7π/2+x)*sinx=√3cosx
2cosx*sinx-√3cosx=0
cosx(2sinx-√3)=0
cosx=0 или 2sinx-√3=0
x=π/2+πn, n∈Z sinx=√3/2
x=(-1)^n*π/3+πn, n∈Z
[-7π;-6π]
x=-7π+π/2=-14π/2+π/2=-13π/2
Ответ: -13π/2
(2sinxcosx+4cosx)-(2√3sin²x+4√3sinx)=0
2cosx(sinx+2)=2√3sinx(sinx+2)=0
2(sinx+2)(cosx-√3sinx)=0
sinx+2=0 или cosx-√3sinx=0 |:cosx≠0
sinx≠2, т.к. 1-√3tgx=0
|sinx|≤1, a 2>1 tgx=√3/3
x=π/6+πn, n∈Z
[-π/2;π]
x=π/6
Ответ: π/6
-2sin(7π/2+x)*sinx=√3cosx
2cosx*sinx-√3cosx=0
cosx(2sinx-√3)=0
cosx=0 или 2sinx-√3=0
x=π/2+πn, n∈Z sinx=√3/2
x=(-1)^n*π/3+πn, n∈Z
[-7π;-6π]
x=-7π+π/2=-14π/2+π/2=-13π/2
Ответ: -13π/2
0
·
Хороший ответ
16 января 2023 23:21
Остались вопросы?
Еще вопросы по категории Алгебра
.В период распродажи магазин снижал цены дважды: в первый раз на 30%, во второй – на 45%. Сколько рублей стал стоить чайник после второго снижения цен...
Исследуйте функцию f(x)=x³-3x на монотонность экстремум и построить ее график....
Найти сумму углов выпуклого 12-ти угольника...
Сколько процентов составляет число 8 от числа 200...
Найдите tg a, если tg(пи/4+а)=-2...