Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
3 апреля 2023 09:26
1159
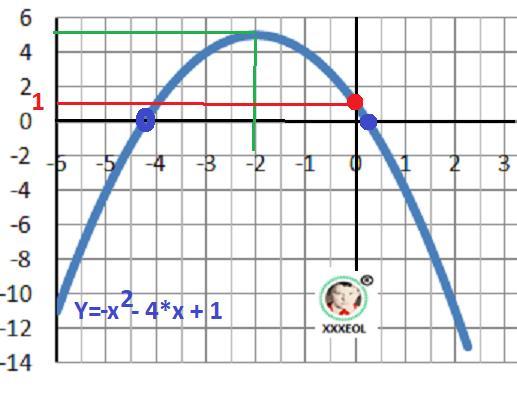
Используя результаты в задании 1б, постройте график функции f(x)=-x²-4x+1. Найдите по графику:а)нули функции; промежутки, в которых f(x)<0 и f(x)>0. б)промежутки возрастания и убывания функции; наибольшее её значение
1
ответ
ДАНО: f(x) = -x² - 4*x + 1.
Объяснение:
Рисунок с графиком функции в приложении.
1) Область определения функции - ООФ - непрерывная, гладкая.
D(f) = R, D(f)=(-∞;+∞)
2) Нули функции - решаем квадратное уравнение.
D = b² - 4*a*c = -4² - 4*(-1)*(1) = 20 - дискриминант. √D = 2√5.
Вычисляем корни уравнения.
x₁ = (-b+√D)/(2*a) = (4+2√5)/(2*(-1)) = = -(2+2√5) - первый корень (-4,24)
x₂ = (-b-√D)/(2*a) = (4- 2√5)/(2*(-1)) = (-2 +2√5 - второй корень (0,24)
Пересечение с осью ОХ: нули функции: -4,24 и 0,24 - корни уравнения.
Пересечение с осью ОУ: f(0) = 1.
Интервалы знакопостоянства.
Положительна: между нулями - х=(-4,24;0,24)
Отрицательна: вне нулей. х=(-∞;-4,28)∪(0,24;+∞)
Поиск экстремума по первой производной.
f'(x) = -2*x - 4 = 0
x = 0 - точка максимума.
Локальный экстремум - максимум - Fmax(-2) = 5
Возрастает: х=(-∞;-2), убывает: х=(-2;+∞)
Объяснение:
Рисунок с графиком функции в приложении.
1) Область определения функции - ООФ - непрерывная, гладкая.
D(f) = R, D(f)=(-∞;+∞)
2) Нули функции - решаем квадратное уравнение.
D = b² - 4*a*c = -4² - 4*(-1)*(1) = 20 - дискриминант. √D = 2√5.
Вычисляем корни уравнения.
x₁ = (-b+√D)/(2*a) = (4+2√5)/(2*(-1)) = = -(2+2√5) - первый корень (-4,24)
x₂ = (-b-√D)/(2*a) = (4- 2√5)/(2*(-1)) = (-2 +2√5 - второй корень (0,24)
Пересечение с осью ОХ: нули функции: -4,24 и 0,24 - корни уравнения.
Пересечение с осью ОУ: f(0) = 1.
Интервалы знакопостоянства.
Положительна: между нулями - х=(-4,24;0,24)
Отрицательна: вне нулей. х=(-∞;-4,28)∪(0,24;+∞)
Поиск экстремума по первой производной.
f'(x) = -2*x - 4 = 0
x = 0 - точка максимума.
Локальный экстремум - максимум - Fmax(-2) = 5
Возрастает: х=(-∞;-2), убывает: х=(-2;+∞)
0
·
Хороший ответ
5 апреля 2023 09:26
Остались вопросы?
Еще вопросы по категории Алгебра
Решите уравнение 2sin^2x-sinx=0...
Вероятность того, что батарейка бракованная, равна 0,03. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вер...
Известно, что B больше А и меньше 0. Выберите наименьшее из чисел. В ответе укажите номер правильного варианта. 1) а-1 2) b-1 3)...
4tg^2 (x) - 3/(sin (3pi/2+x)) +3 = 0...
Дана арифметическая прогрессия: 33;25;17;Найдите первый отрицательный член этой прогрессии...