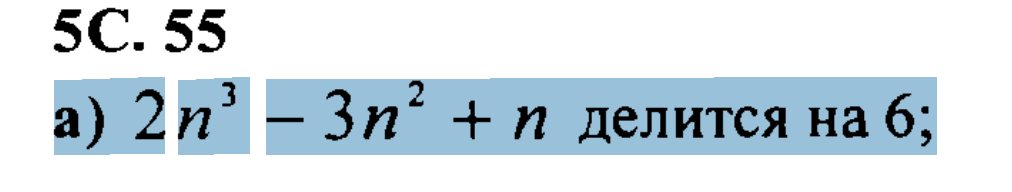Докажите что при любом натуральном n

Проверим для n=1
n^3+3n^2+5n+3=12 делится на 3, утверждение верно для n=1

n^3+3n^3+5n+3=12 делится на 3, утверждение верно для n=1
Пусть утверждение верно для всех n≤k, докажем его для n=k+1
(k+1)^3+3(k+1)^2+5(k+1)+3=
=k^3+3k^2+3k+1+3*(k^2+2k+1)+5k+5+3=
=k^3+3k^2+5k+3+3k^2+9k+9=
=(k^3+3k^2+5k+3)+3(k^2+3k+3)
(k^3+3k^2+5k+3) делится на 3 по предположению индукции, 3(k^2+3k+3) делится на 3, следовательно утверждение верно для n=k+1, следовательно утверждение верно для любых натуральных n.
Для тройки:
(k+1)^3+3(k+1)^3+5(k+1)+3=
=4(k^3+3k^3+3k+1)+5k+5+3=(4k^3+5k+3)+3*(4k^2+4k+3)
(4k^3+5k+3) делится на 3 по предположению индукции, 3*(4k^2+4k+3) делится на 3, следовательно утверждение верно для n=k+1, следовательно утверждение верно для любых натуральных n.

2. Метод математической индукции.
Проверим для n=2
2n^3-3n^2+n=6 делится на 6, утверждение верно для n=2
Пусть утверждение верно для всех n≤k, докажем его для n=k+1
2(k+1)^3-3(k+1)^2+(k+1)=
=2(k^3+3k^2+3k+1)-3(k^2+2k+1)+k+1=
=(2k^3-3k^2+k)+6k^2
(2k^3-3k^2+k) делится на 6 по предположению индукции, 6k^2 делится на 6, следовательно утверждение верно для n=k+1, следовательно утверждение верно для любых натуральных n.

Второй способ. Разложение на множители.
1. n^3+3n^2+5n+3=
=n^3+3n^2+3n+1+2n+2=
=(n+1)^3+2(n+1)=(n+1)((n+1)^2+2)=
=(n+1)(n^2+2n+3)=(n+1)(n(n+2)+3)=
=n(n+1)(n+2)+3(n+1)
n(n+1)(n+2) - произведение 3 последовательных чисел, делится на 3
3(n+1) делится на 3, следовательно вся сумма делится на 3.

2. 2n^3-3n^2+n=n(2n^2-3+1)
n=1 корень выражения в скобках, следовательно можно вынести (n-1)
n(2n^2-3+1)=n(n-1)(2n-1)=
=n(n-1)(2(n+1)-3)=2n(n-1)(n+1)-3n(n-1)
Из 2 последовательных чисел одно делится на 2, а из трех одно делится на 3, следовательно 2n(n-1)(n+1) делится на 6 и 3n(n-1) делится на 6