Прошу помогите плиз... В гладкий высокий стакан радиусом 4 см поставили палочку длиной 10 см и массой 90 г. До какой высоты h надо налить в стакан жидкость, плотность которой составляет 0,75 плотности материала палочки, чтобы сила, с которой верхний конец палочки давит на стенку стакана, равнялась 0,4 Н?

1 ответ

Посмотреть ответы

Megamozg

2205

Ответ: 4 см

Объяснение:
Дано:
R = 4 см = 0.04 м
L = 10 см = 0.1 м
m = 90 г = 0.09 кг
$\rho_ = 0.75\rho$ ( $\rho_$ - плотность жидкости) ( $\rho$ - плотность материала палочки)
F = 0.4 Н
-------------------------------------------------------
h - ?
Решение:
(Смотри рисунок)
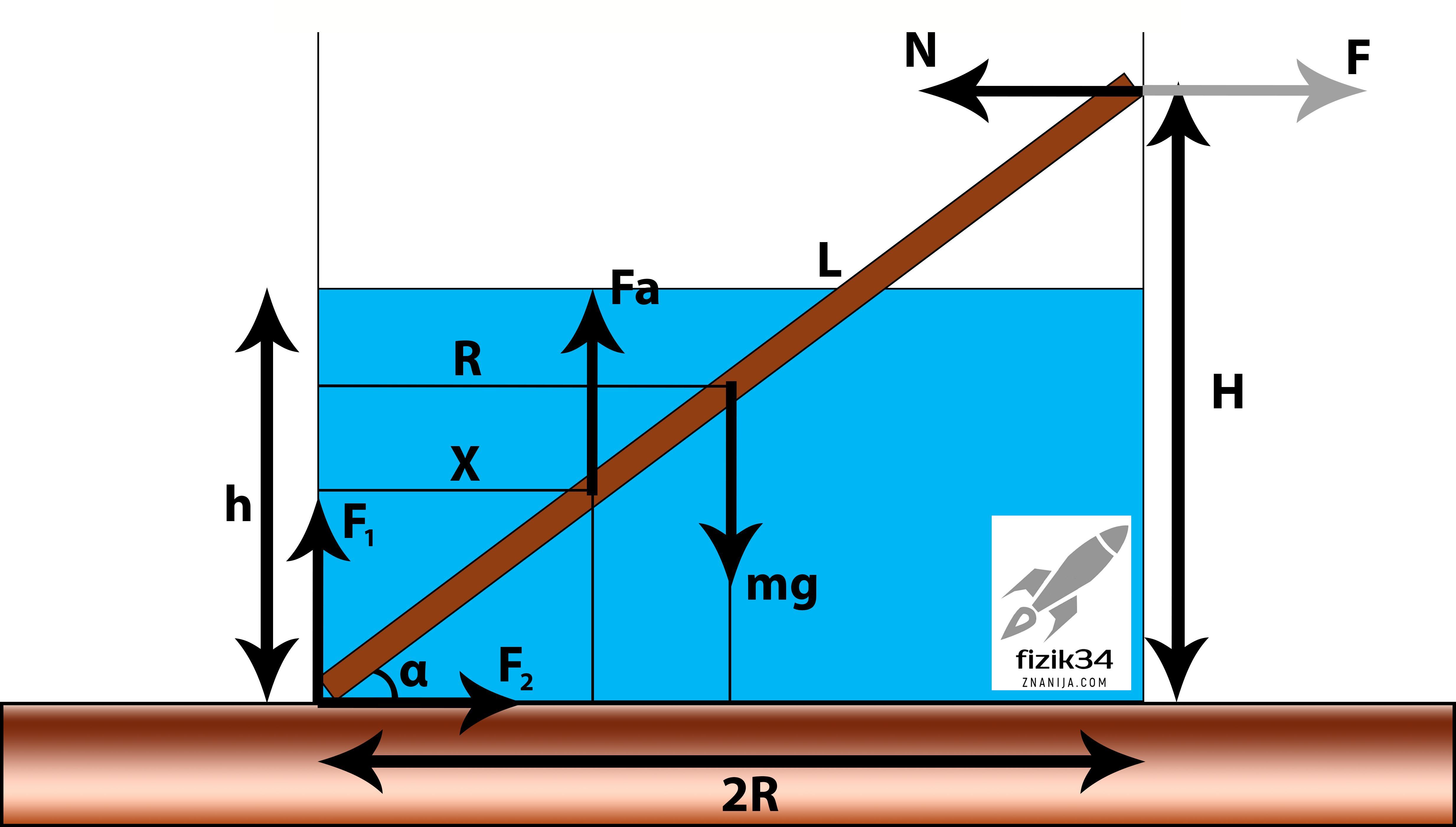
Расставим все силы действующие на палочку.
Fa - сила архимеда, действующая со стороны жидкости на частично погруженную в неё палочку
mg - сила тяжести, действующая со стороны Земли
N - сила реакции опоры, действующая со стороны стакана на верхний конец палочки. ((Причем, прошу заметить, что согласно 3-ему закону Ньютона |F| = |N| = 0.4 Н) работать мы будем именно с N, а не F, ведь мы рассматриваем силы действующие на палочку, а не на стакан.)
$F_$ и $F_$ - также силы реакций опоры, действующие со стороны стакана, но уже на нижний конец палочки.
В нашем случае, когда палочка покоиться, мы можем попробовать абстрагироваться от неизвестных сил реакций опор $F_$ и $F_$ и записать равенство моментов известных нам сил действующих на палочку.
Отсюда $M_ - M_ - M_ =0$
$M_ = M_ + M_$
Где

$M_ = mgR$ (момент силы действующий на палочку со стороны силы тяжести)
$M_ = NH$ (момент силы действующий на палочку со стороны силы реакции опоры). Из теоремы Пифагора $H = \sqrt-4R^ }$ , тогда $M_ = N\sqrt-4R^ }$ .
$M_ =\rho_ gVX$ (момент силы действующий на палочку со стороны силы Архимеда); V - объем погруженной части палочки: $V=V_ \dfrac$ ; $V_$ - общий объем палочки: $V_ = \dfrac{\rho}$ , отсюда $V= \dfrac{\rho H}$ , тогда $M_ =\dfrac{\sqrt-4R^ }}X$ . Из рисунка видно, что $X = \dfrac ctg\alpha$ , $\dfrac$ потому что сила Архимеда приложена к центру объема погружной части тела. Также, из рисунка $ctg\alpha = \dfrac$ ⇒ $ctg\alpha = \dfrac{\sqrt-4R^}}$ , значит $X = \dfrac{\sqrt-4R^}}$ , поэтому $M_ = \dfracR}-4R^}$

Из всего выше сказанного $mgR=\dfracR}-4R^}+N\sqrt-4R^ }$
$\dfracR}-4R^} = mgR - N\sqrt-4R^ }$
$h=\sqrt{\dfrac{(L^-4R^)(mgR - N\sqrt-4R^})} }$
$h=\sqrt{\dfrac{(0.1^-4*0.04^)(0.09*10*0.04 - 0.4\sqrt-4*0.04^})} } =0.04$ м = 4 см

Хороший ответ

17 января 2023 01:47

Остались вопросы?

Найти нужный

Еще вопросы по категории Физика

10.каждая строка таблицы описывает физические параметры одной электрической цепи. определите недостающие значения в таблице. ответы запишите в порядке... абсолютный показатель преломления алмаза 2.42 какова скорость света в алмазе ? скорость света в воздухе С=3*10 ^8 м/с?... в одном месте магнитные линии расположены гуще чем в другом. Какой вывод о величине магнитного поля можно сделать на основании этого... №4 Чему равна скорость распространения электромагнитной волны? А: 340 м/с Б: 340 км/с ........................ 1)пластины плоского конденсатора присоединяют к источнику напряжение в 220 вольт. Ёмкость кондесатора равна 1,5 умножить 10-4 мкФ. Чему будет равен за...