Диагональ правильной четырехугольной призмы образует с плоскостью боковой грани угол в 30°. Найдите угол между диагональю и плоскостью основания.Помогите решить подробно и с рисунком.

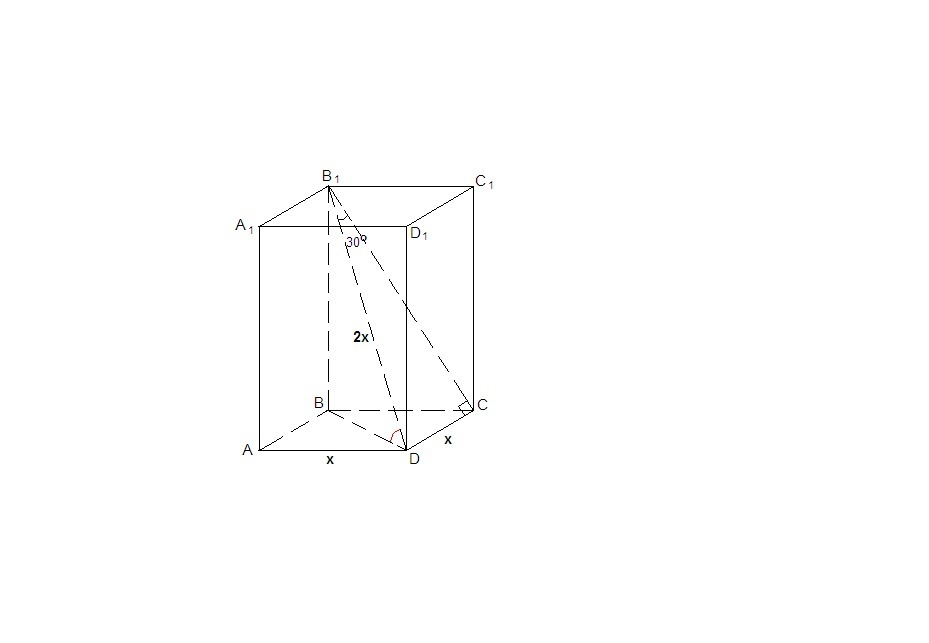
Призма правильная, значит в основании лежит квадрат, а боковые грани - равные прямоугольники.
DC⊥BCC₁, значит В₁С - проекция диагонали B₁D на плоскость ВСС₁, тогда
∠DB₁C = 30°.
Пусть х - сторона основания, тогда BD = x√2 как диагональ квадрата.
ΔDB₁C: ∠DCB₁ = 90°, ∠DB₁C = 30°, DC = x, тогда B₁D = 2x.
В₁В⊥АВС, BD - проекция B₁D на плоскость основания, тогда ∠B₁DB - искомый.
ΔB₁DB: ∠B₁BD = 90°, cos∠B₁DB = BD / B₁D
cos∠B₁DB = x√2 / (2x) = √2/2, ⇒
∠B₁DB = 45°