Лучшие помощники

Megamozg 2205 б
Matalya1 1800 б
DevAdmin 1720 б
arkasha_bortnikov 900 б
Dwayne_Johnson 870 б

Показать еще

·

Геометрия

27 декабря 2022 10:21

9174

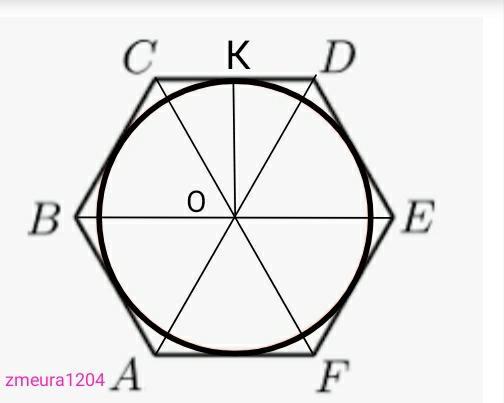
Найдите радиус окружности, вписанной в правильный шестиугольник со стороной √3.

1 ответ

Посмотреть ответы

Ответ:

r=1,5
Объяснение:
ОК- высота ∆СОD
OK=r
CO=√3 сторона равностороннего треугольника ∆СОD
OK=CO√3/2=√3*√3/2=1,5

Zmeura1204

0

·

Хороший ответ

29 декабря 2022 10:21

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Найдите площадь прямоугольника , если его периметр равен 44 и одна сторона на 2 больше другой .... В треугольнике АВС из прямого угла С провели биссектрису СМ и высоту СН так, что угол МСН равен 15 . Найдите меньший катет АС и отрезок АН , если гипо... А1.Какая область не пересекается рекой Волгой? 1)Ульяновская 2)Пензенская 3)Самарская 4)Волгоградская А2.Укажите верную последовательность природных... Найдите синус угла АОВ. В ответ укажите значение синуса, умноженное на 2 корня из 2-х.... Какие из следующих утверждений верны? 1) у любой трапеции основания параллельны 2) все углы ромба равны 3) Две окружности пересекаются если радиус...