Помогите прошу. в правильной четырехугольной пирамиде sabcd все ребра равны 1. Найдите угол между прямыми а)AB и SCAnd SB и SD

1 ответ

Посмотреть ответы

Megamozg

2205

ОТВЕТ: угол между прямыми AB и SC равен 60°
угол между прямыми SB и SD равен 90°
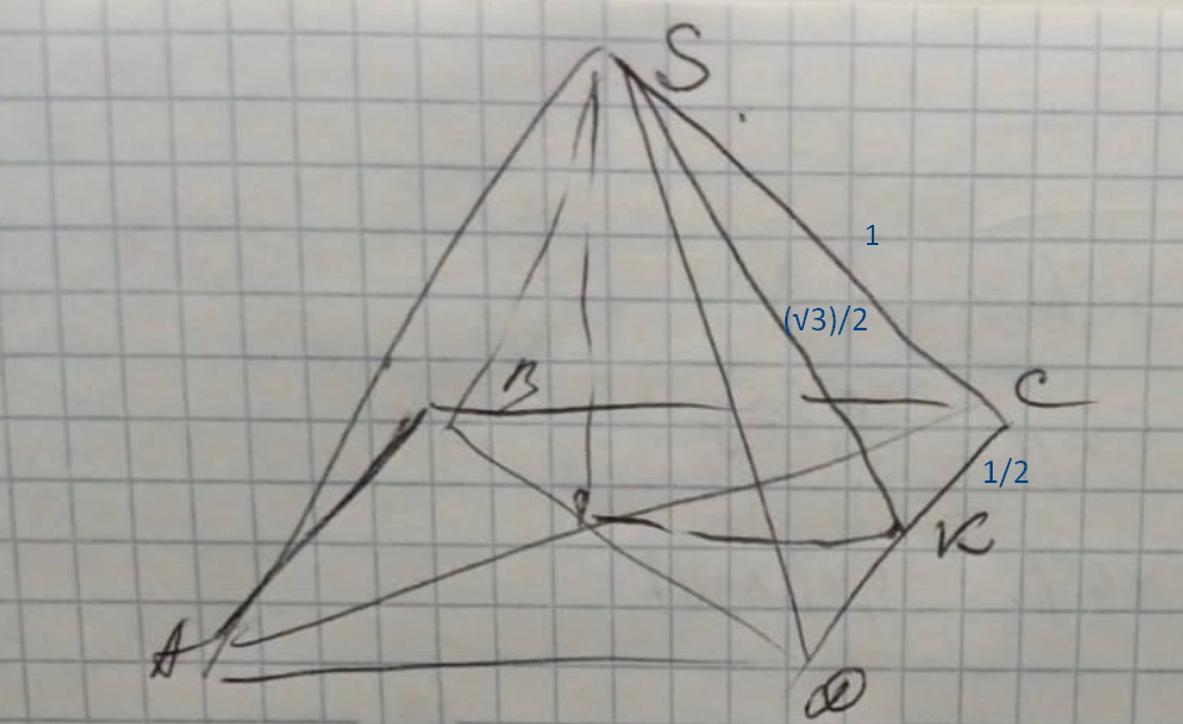
Условие: В правильной четырехугольной пирамиде Sabcd все ребра равны 1.
Найти: угол между прямыми а)AB и SC ; б) SB и SD
РЕШЕНИЕ:
1) АС=a√2=√2;
2) ΔSKC, ∠К=90°, $\displaystyle SK = \sqrt \bigg)^2} = \sqrt } =\sqrt{\frac-\frac }=\sqrt{\frac } =\frac{\sqrt }$
3) ∠(AB;SC) =∠(DC;SC)= ∠SCD, т.к АВ║СD (угол между скрещивающимися прямыми равен углу, между соответственно параллельными прямыми)
cos∠SCK = CK/SC = 1/2 : 1 =1/2
4) Если cos∠SСК=1/2 , то ∠SСК=60°
(.)К середина СD т.е SK - медиана ΔDSC.
ΔDSC- равносторонний, т.к все рёбра пирамиды равный 1. Медиана SK является высотой в равнобедренном и равностороннем треугольнике.
5) Рассмотрим ΔBSD
SB=1 , SD=1 , BD=AC=√2
по теореме косинусов:
BD²=SB²+SD²-2SB*SDcosS
(√2)²=1²+1²-2*1*1*cosS
2=2-2*cosS
2*cos∠S=2-2
2*cos∠S=0 ⇒ cos∠S=0, т.е ∠S=90°
∠BSD= ∠(BS;SD) = 90°

Удачи!

Хороший ответ

17 января 2023 02:16

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Радиус окружности , вписанной в прямоугольный треугольник , равен полуразности его катетов . Найти отношение большего катета к меньшему... Треугольник LMN,вписанный в окружность,делит ее на три дуги.Вычисли угол LON и углы треугольника LMN,если даны два центральных угла:∢LOM=140° и ∢MON=1... А) На прямой n отметьте точки А, В и С так, чтобы выполнялось равенство АС - ВС = АВ б) Постройте лучи EA, EB, EC так, чтобы выполнялось равенство ∠A... Окружность S, вписанная в равнобедренный треугольник АВС , касается боковых сторон АВ и ВС соответственно в точках К и L, и касается основания АС в то... Верно ли что Если прямая перпендикулярна двум противоположным сторонам параллелограмма, то она перпендикулярна плоскости параллелограмма....