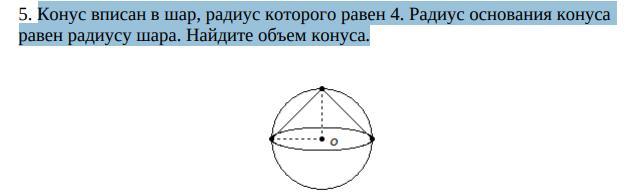
Конус вписан в шар, радиус которого равен 4. Радиус основания конуса равен радиусу шара. Найдите объем конуса.

1 ответ

Посмотреть ответы

DevAdmin

1720

Дано:

Конус вписан в шар.
R шара, конуса = 4

Найти:

V - ?

Решение:

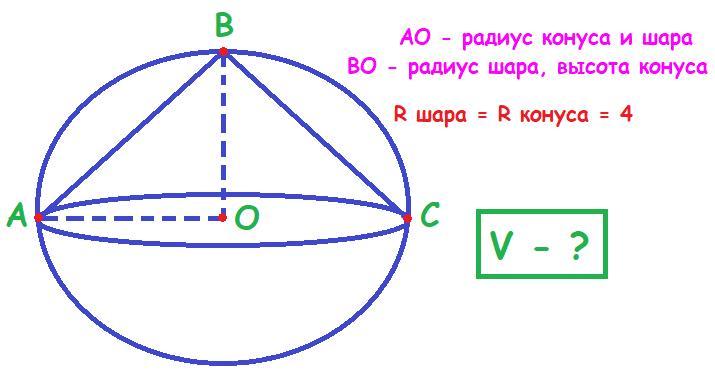
Обозначим точки, изображенные на рисунке, буквами А, В и С.
Так как АО и ОВ - радиусы шара ⇒ АО = ОВ = 4.
AO также радиус конуса, который вписан в шар.
ОВ также высота конуса, который вписан в шар.
V = 1/3пR²h, где R - радиус конуса; h - высота конуса ⇒ V = п(1/3 * 4² * 4) = 64/3 =21 1/3п см³.

Ответ: 21 1/3п см³.

Хороший ответ

17 января 2023 04:08

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Сумма вертикальных углов МОЕ и DOC, образованных при пересечении прямых MC и DE, равна 204° . Найдите угол MOD... Итоговый зачёт 8 класс Карточка 1 1.Определение выпуклого многоугольника. Сумма его внутренних углов. 2.Касательная к окружности. Теорема о свойств... Один из углов прямоугольного треугольника равен 60 ,а сумма гипотенузы и меньшего катита ровна 42 см. найдите гипотенузу Буду рада ,и благодарна если... Укажите номера верных утверждений.1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.2) Вертика... Одна из диагоналей параллелограмма является высотой и равна 9 см. Найдите стороны этого параллелограмма, если его площадь равно 108 см....