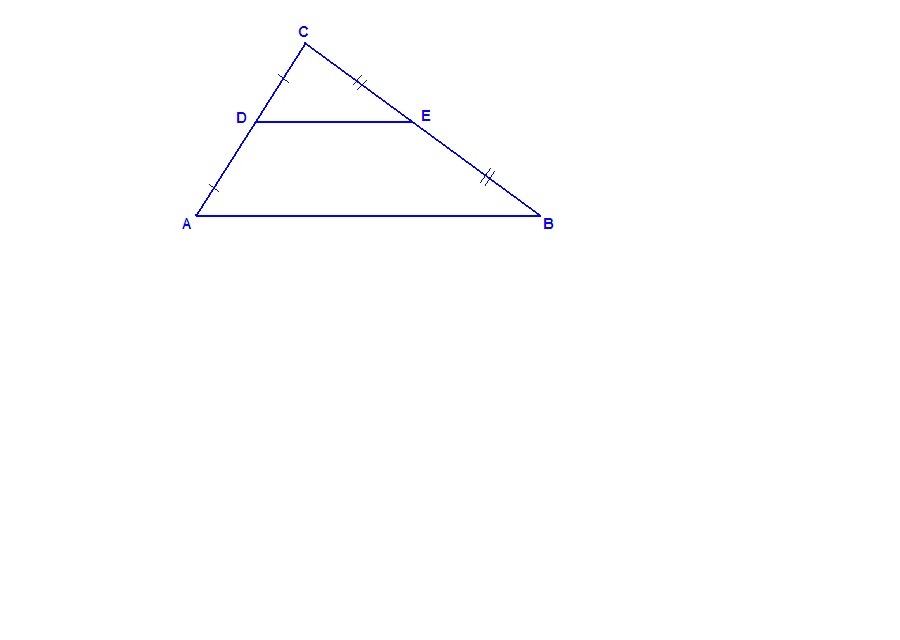
В тре­уголь­ни­ке ABC известно, что DE — сред­няя линия. Пло­щадь тре­уголь­ни­ка CDE равна 12. Най­ди­те пло­щадь тре­уголь­ни­ка ABC.

Средняя линия параллельна третьей стороне треугольника и равна ее половине:
DE║AB, DE = 1/2 AB.
∠CDE = ∠CAB как накрест лежащие углы при пересечении параллельных прямых DE и АВ секущей АС,
угол при вершине С общий для треугольников АВС и DEC, значит эти треугольники подобны по двум углам.
k = DE/AB = 1/2
Отношение площадей подобных треугольников равно квадрату коэффициента подобия:
Sdec : Sacb = k² = 1 : 4
Sabc = 4Sdec = 4 · 12 = 48