Докажите теорему что все точки каждой из двух параллельных прямых равноудалены от другой прямой

Расстояние между двумя параллельными прямыми есть длина перпендикуляра, опущенного из некой точки одной прямой на другую.
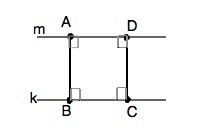
. Пусть даны параллельные прямые m и k
Возьмём на прямой m произвольную точку А и проведем через неё перпендикуляр до пересечения с прямой k в точке В
Так как если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой, то углы, образованные отрезком АВ - и прямыми m и k - прямые.
Таким же образом выберем на некотором расстоянии от т.А точку D и проведем через неё перпендикуляр DC, который образует с прямыми m и k прямые углы.
Четырёхугольник АВСD- прямоугольник (все углы прямые). Так как в прямоугольнике противоположные стороны равны, АВ=СD, т.е точки А и D на прямой m равноудалены от прямой k. =>
Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
-------------
Существуют и другие доказательства. Попробуйте найти их самостоятельно.