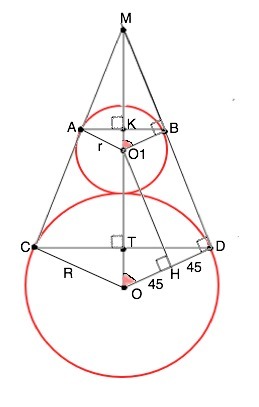
Окружности радиусов 45 и 90 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D на второй .При этом AC и BD – общие касательные окружностей. Найдите расстояние между прямыми AB и CD.

Продлим касательные до их пересечения в точке М.
Центры О и О₁ касающихся окружностей лежат на биссектрисе МО угла СМD.

r =O₁B=45, R=OD=90.
Радиусы О₁В и ОD, проведенные в точки касания, перпендикулярны касательной МD (свойство радиусов).
Из О₁ проведем О₁Н ║ МD. В параллелограмме О₁ВDО ∠В=∠D= 90°, следовательно, О₁ОDВ - прямоугольник.
HD=O₁B, ОН=90-45=45.
Прямоугольные ∆ МО₁В и ∆ МОD подобны по общему острому углу при М.
ОО₁=R+r=90+45=135
Косинус равных углов при О и О₁=ОН/ОО₁=45/135=1/3.
Тогда КО₁=О₁В•cos KO₁B=45•1/3=15
TO=DO•cos TOD=90•1/3=30
Расстояние между АВ и СD равно
КТ=ОО₁-ТО+КО₁=135-30+15=120 (ед. длины)