Дана четырёхугольная пирамида,в основании которой лежит ромб.Все высоты боковых граней,проведённые из вершин,равны 53.Высота пирамиды равна 45.Острый угол ромба,лежащего в основании,равен 60 градусов.Найди площадь основания пирамиды.

1 ответ

Посмотреть ответы

Megamozg

2205

Ответ:
$\dfrac}$ кв. ед.
Объяснение:
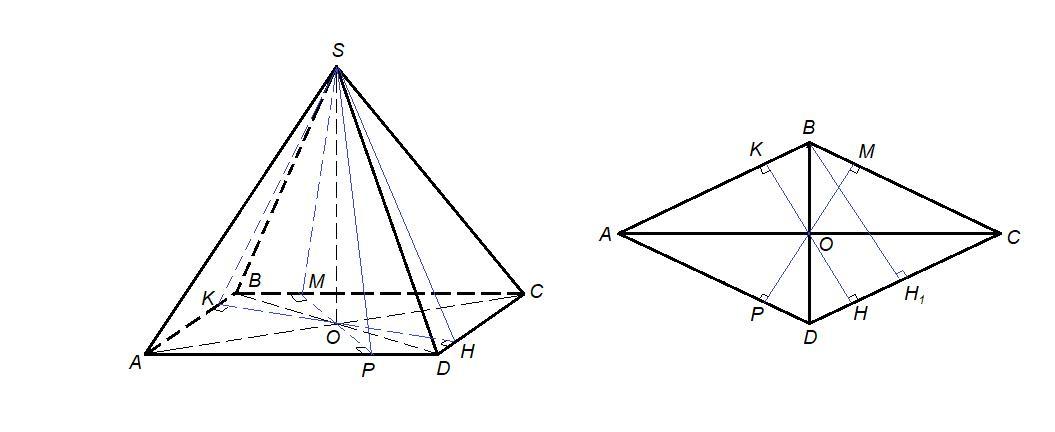
Основание четырехугольной пирамиды - ромб.
SO = 45 - высота пирамиды.
Проведем перпендикуляры к сторонам основания из точки О:
OK⊥AB, OM⊥BC, OH⊥CD, OP⊥AD.
Отрезки ОК, ОМ, ОН, ОР - проекции соответствующих наклонных на плоскость основания, значит SK⊥AB, SM⊥BC, SH⊥CD, SP⊥AD по теореме о трех перпендикулярах.
По условию SK = SM = SH = SP = 53, значит и
ОК = ОМ = ОН = ОР как проекции равных наклонных, проведенных из одной точки.
Тогда точка О равноудалена от сторон ромба, то есть О - центр вписанной в ромб окружности (точка пересечения диагоналей).
ΔSOH: ∠SOH = 90°, по теореме Пифагора
OH = √(SH² - SO²) = √(53² - 45²) = √((53 - 45)(53 + 45)) =
= √(8 · 98) = √(2 · 4 · 2 · 49) = 2 · 2 · 7 = 28
КН = 2 · ОН = 2 · 28 = 56
ВН₁ = КН = 56 как расстояния между параллельными прямыми
∠BCD = 60°, BC = CD, значит ΔBCD равносторонний.
ВН₁ - высота равностороннего треугольника, тогда
$BH_1=\dfrac}$
$CD=\dfrac{\sqrt}=\dfrac{\sqrt}=\dfrac{\sqrt}$
Площадь ромба:
$S=a^2\cdot \sin \alpha$
$a=CD=\dfrac{\sqrt}$
$\alpha =60^\circ$
$S=\left(\dfrac{\sqrt}\right)^2\cdot \dfrac{\sqrt}=\dfrac}$

Хороший ответ

17 января 2023 10:20

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Начертите неразвернутый угол AOB и проводите:1) луч OC, который делит угол AOB на две части; 2) луч OD, который не делит угол AOB на два угла.... Сколько общих точек могут иметь две прямые... Большая высота параллелограмма равна 6. Найдите площадь параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на отрезки... Все формулы по геометрии за 7 класс... Какое из следующих утверждений верно? 1)В прямоугольном треугольнике гипотенуза равна сумме катетов 2) Один из двух смежных углов острый а другой тупо...