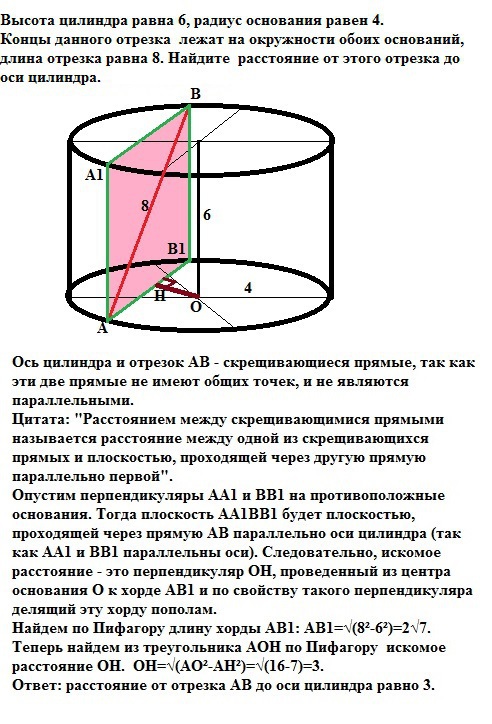
высота цилиндра равна 6 радиус основания равен 4.Концы данного отрезка лежат на окружности обоих оснований длина отрезка равна 8.Найдите расстояние от этого отрезка до оси цилиндра

1 ответ

Посмотреть ответы

Megamozg

2205

Ось цилиндра и отрезок АВ - скрещивающиеся прямые, так как эти две прямые не имеют общих точек, и не являюnся параллельными.
Цитата: "Расстоянием между скрещивающимися прямыми называется расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой".
Опустим перпендикуляры АА1 и ВВ1 на противоположные основания. Тогда плоскость АА1ВВ1 будет плоскостью, проходящей через прямую АВ параллельно оси цилиндра (так как АА1 и ВВ1 параллельны оси). Следовательно, искомое расстояние - это перпендикуляр ОН, проведенный из центра основания О к хорде АВ1 и по свойству такого перпендикуляра делящий эту хорду пополам.
Найдем по Пифагору длину хорды АВ1: АВ1=√(8²-6²)=2√7. Теперь найдем из треугольника АОН по Пифагору искомое расстояние ОН. ОН=√(АО²-АН²)=√(16-7)=3.
Ответ: расстояние от отрезка АВ до оси цилиндра равно 3.

Хороший ответ

17 января 2023 12:26

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Работа по геометрии Срочно!!! 9 класс 1. дано точки А(3;-4), С(-2;5). найдите : 1) координаты векторов ВА и ВС. 2) модули векторов ВА и ВС. 3. докажи... Периметр ромба равен 24, а косинус одного из углов равен 2√2/3. Найдите площадь ромба.... Вершины треугольника АВС лежат на сфере радиуса 17,12 см. Найдите расстояние от центра сферы до плоскости треугольника, если АВ= 16 см, ВС=30 см, АС-... Две стороны треугольника параллельны плоскости \alpha . Докажите,что и третья сторона параллельна плоскости \alpha.... Чему равна сумма углов правильного восьмиугольника...