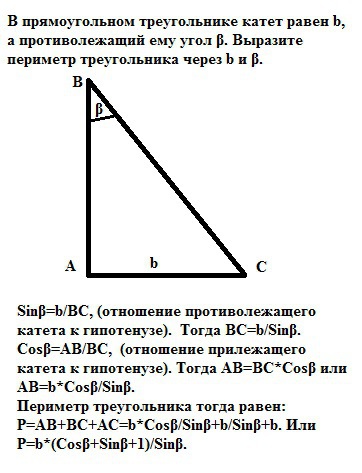
в прямоугольном треугольник катет равен b, а противолежащий ему угол β. выразите периметр треугольника через b и β

1 ответ

Посмотреть ответы

Megamozg

2200

Sinβ=b/BC, (отношение противолежащего катета к гипотенузе). Тогда ВС=b/Sinβ.
Cosβ=AB/BC, (отношение прилежащего катета к гипотенузе). Тогда АВ=ВС*Cosβ или
АВ=b*Cosβ/Sinβ.
Периметр треугольника тогда равен:
Р=АВ+ВС+АС=b*Cosβ/Sinβ+b/Sinβ+b. Или
Р=b*(Cosβ+Sinβ+1)/Sinβ. Это ответ.

Хороший ответ

4 апреля 2023 21:32

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Осевым сечением цилиндра является квадрат, площадь которого равна 144 см^2 . Вычислите площадь боковой поверхности цилиндра... КАК НАЗЫВАЕТСЯ ФИГУРА ???? Не ромб, ибо не все стороны равны, а как ?... Свойства вписанного угла. Формулировка и доказательство... Чем отличаются правильная четырехугольная призма и прямоугольный параллелепипед? приведите пример.... В кубе 𝐴𝐵𝐶𝐷𝐴1𝐵1𝐶1𝐷1 найдите угол между: 𝐴𝐵 и 𝐴1𝐵1 𝐴𝐵 и 𝐴1𝐵 𝐴𝐵 и 𝐶1𝐶 𝐴𝐵 и 𝐶1𝐵 (𝐴𝐵𝐶) и (𝐵1𝐶1𝐷1) (𝐴𝐵𝐶) и (𝐵1𝐶1𝐵)...