в прямоугольном треугольнике биссектриса острого угла делит противоположный катет на отрезки длиной 4 и 5 . определить площадь треугольника.

1 ответ

Посмотреть ответы

Megamozg

2205

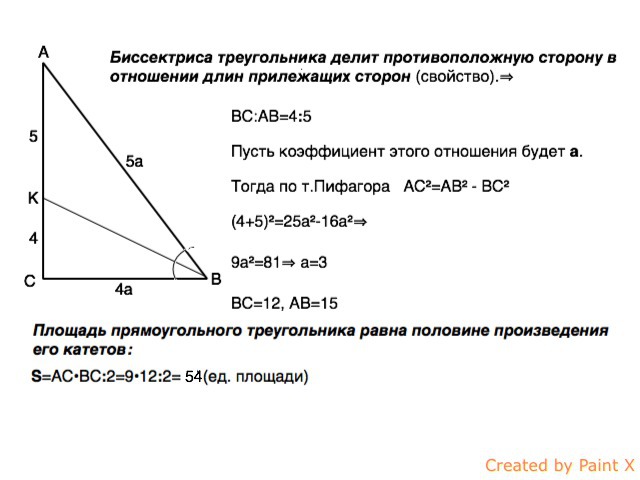
Обозначим данный треугольник АВС,
∠С=90°, ВК- биссектриса, СК=4, КА=5.
Биссектриса треугольника делит противоположную сторону в отношении длин прилежащих сторон (свойство).⇒
ВС:АВ=4:5
Пусть коэффициент этого отношения будет а.
Тогда по т.Пифагора
АС²=АВ² - ВС²
(4+5)²=25а²-16а²⇒
9а²=81⇒
а=3
ВС=12, АВ=15
Площадь прямоугольного треугольника равна половине произведения катетов:
S=АC•ВC:2=9•12:2=54 (ед. площади)

Хороший ответ

17 января 2023 12:27

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

На биссектрисе угла А взята точка D, а на сторонах этого угла - точки В и С такие, что угол ADB равен углу DCA. Доказать, что треугольник ABD рав... Периметр равнобедренного треугольника равен 216, а боковая сторона-78. Найдите площадь треугольника.... Перерисуйте рисунок 7.Постройте отрезки,симметричные отрезкам AB и CD относительно прямой m.Даю 32 баллов ПЛЖАЛУЙСТА ПОМОГИТЕ... В треугольнике abc ad биссектриса,угол с равен 50,угол cad равен 28.найдите угол В... В треугольнике MNP точка К лежит на отрезке MN, причем NKP – острый угол. Докажите, что KP < MP....