Отрезок АВ, концы которого лежат на арзных окружностях оснований цилиндра, пересекает ось цилиндра под углом 30 градусов. Найти объем цилиндра, если отрезок АВ = 4 корня из 3

1 ответ

Посмотреть ответы

Megamozg

2205

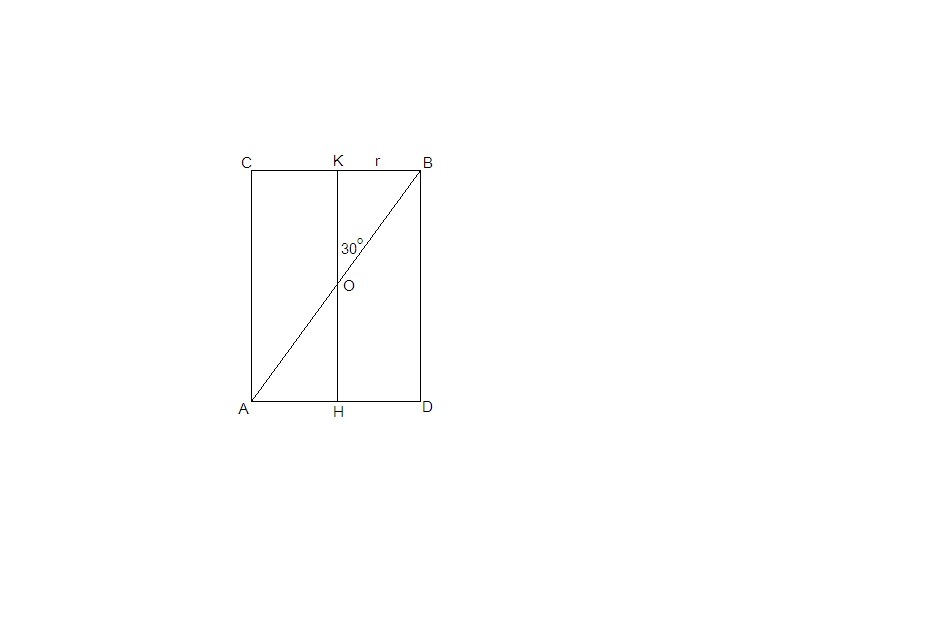
Т.к. отрезок АВ пересекает ось цилиндра, они лежат в одной плоскости. Осевое сечение цилиндра на рисунке.
ΔКОВ = ΔНОА по катету и прилежащему острому углу (KB = AH = r, ∠КОВ = ∠НОА как вертикальные) ⇒ КО = ОН, АО = ОВ = АВ/2 = 2√3
ΔКОВ:
∠ОКВ = 90°, КВ = ОВ/2 = √3 как катет, лежащий напротив угла в 30°.
r = √3
ОК = ОВ·cos30° = 2√3·√3/2= 3 ⇒ KH = 6
h = 6 высота цилиндра
V = Sосн · h = πr²·h = π · 3 · 6 = 18π

Хороший ответ

17 декабря 2022 21:53

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Площади подобных треугольников равны 17 см2 и 68 см2. Сторона первого треугольника равна 8см. Найти сходственную сторону второго треугольника. прошу п... Перерисуйте рисунок 7.Постройте отрезки,симметричные отрезкам AB и CD относительно прямой m.Даю 32 баллов ПЛЖАЛУЙСТА ПОМОГИТЕ... Боковая грань правильной четырехугольной пирамиды наклонена к плоскости основания под углом 60* . Площадь основания пирамиды 16см^2 . Найти апофему... Точка C - середина отрезка AB Точка О- середина отрезка AC 1)Найди AC CB AO OB если AB =2 см 2)Найдите AB AC AO и OB если CB =3.2 см Пожалуйста срочн... Сторона BC треугольника ABC продолжена за точку B. На продолжении отмечена точка D так,что AB=BD. Найдите величину угла BAD,если угол ACВ равен 70*,а...