Докажите основное тригонометрическое тождество.

1 ответ

Посмотреть ответы

Megamozg

2205

sin²α + cos²α = 1
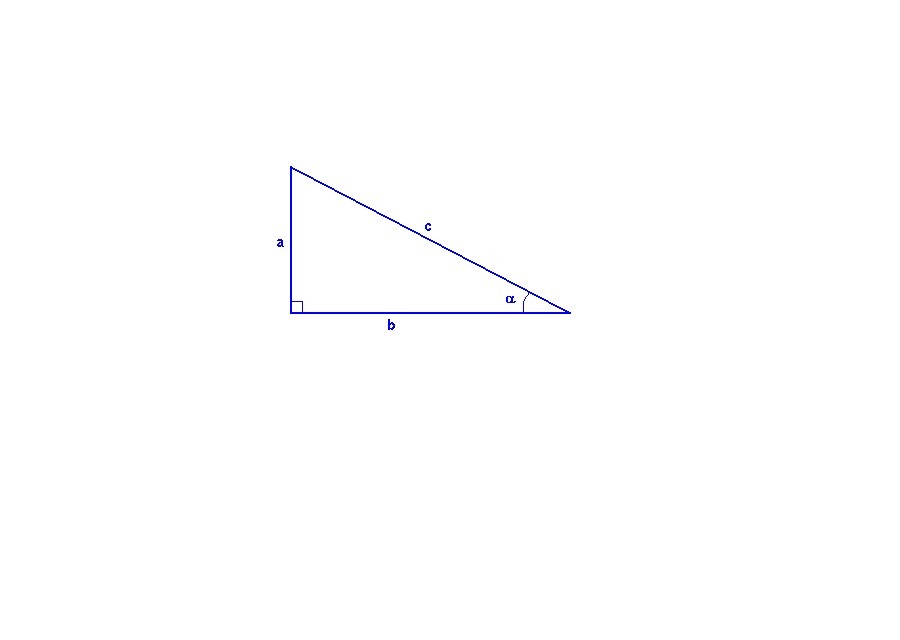
Синус острого угла прямоугольного треугольника - это отношение противолежащего катета к гипотенузе.
Косинус острого угла прямоугольного треугольника - это отношение прилежащего катета к гипотенузе.
sinα = a/c
cosα = b/c
Возведем в квадрат:
sin²α = a² / c²
cos²α = b² / c²
sin²α + cos²α = a² / c² + b² / c² = (a² + b²) / c² = с² / c² = 1,
так как по теореме Пифагора a² + b² = c².

Хороший ответ

4 апреля 2023 02:17

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Треугольки АВС и А1В1С1 подобны,причем стороны АВ и ВС соответствуют сторонам А1В1 и В1С1.Найдите неизвестные стороны этих треугольников,если ВС=5см,А... Даны координаты вершин четырехугольника ABCD: A(-6;1), B(0;5), C(6;-4),D(0,-8). Докажите, что это прямоугольник и найдите координаты точки пересечения... Площадь параллелограмма ABCD равна 6, точка E середина стороны AB. Найдите площадь треугольника AED.... Что называется длиной ненулевого вектора?чему равна длина нулевого вектора?... Помогите решить задачу по геометрии...