Все стороны правильного треугольника касаются сферы диаметром 4 дм, плоскость треугольника удалена на расстоянии 1 дм от центра сферы. Найдите сторону треугольника.

1 ответ

Посмотреть ответы

Megamozg

2180

Все стороны правильного треугольника касаются сферы диаметром 4 дм, плоскость треугольника удалена на расстоянии 1 дм от центра сферы. Найдите сторону треугольника.
Любое сечение сферы плоскостью - окружность.
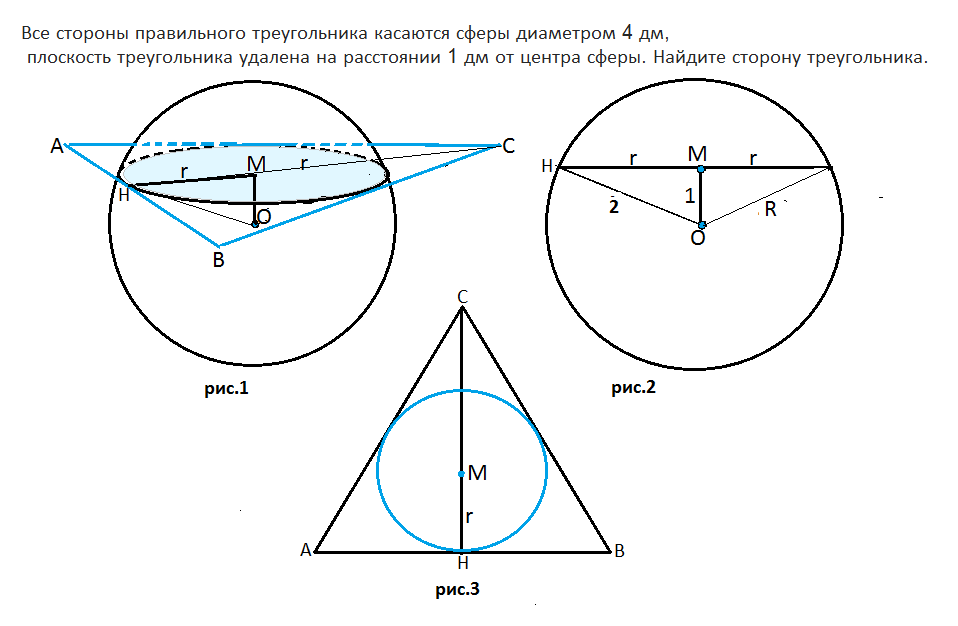
Плоскость треугольника АВС пересекает сферу по линии, являющейся окружностью с центром М (рис.1),
Сделаем схематический рисунок (рис.2)
Т.к. диаметр сферы=4 дм, ее радиус ОН равен 2 дм
ОМ=1 дм, ОН=2 дм
НМ=r
По т.Пифагора
r=√(2²-1²)=√3
Радиус вписанной в правильный треугольник окружности (а сечение сферы - вписанная в данный треугольник окружность) равен 1/3 высоты треугольника. (рис.3)
Тогда высота треугольника СН=3*√3
Сторона правильного треугольника равна частному от деления его высоты на синус 60º
АВ=АС=СВ=[3√3):√3]:2
АВ=6 дм

Хороший ответ

4 апреля 2023 03:27

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

вершины треугольника авс лежат на сфере радиусом 13 см. найдите расстояние от центра сферы до плоскости треугольника, если ав=6, вс=8, ас=10... Треугольники ABC и ADC лежат в разных плоскостях и имеют общую сторону AC. Точка P – середина стороны AD, точка K – середина DC. 1.Каково взаимное рас... Сделайте пожалуйста чертеж детали в трех видах (проекциях)... Помогите пожалуйста! Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=78∘ и ∠OAB=69∘. Найдите угол BCO. Ответ дайте в г... Прямоугольный треугольник MBE (∢M=90°) находится в плоскости α. BE=10 см, а ME=6 см. К этой плоскости проведён перпендикуляр CB длиной 6 см. Вычисли р...