Лучшие помощники
- Megamozg 2205 б
- Matalya1 1800 б
- DevAdmin 1720 б
- arkasha_bortnikov 900 б
- Dwayne_Johnson 870 б
2 апреля 2023 06:23
884
помогите решить задачи про шестиугольную пирамиду 1) В правильной шестиугольной пирамиде SABCDEF сторонаоснования равна корень из 3, а боковое ребро равно 2. Найдите угол SAD. 2) В правильной шестиугольной пирамиде SABCDEF сторона основания равна 1, а высота равна корень из 3. Найдите угол между высотой и боковым ребром. 3) В правильной шестиугольной пирамиде SABCDEF сторона основания равна корень из 3, а боковое ребро равно 3. Найдите угол SAC. 4) В правильной шестиугольной пирамиде сторона основания равна апофеме. Найдите угол между боковой гранью и основанием.
1
ответ
Ответ:
1) ∠SAD = 30°.
2) ∠ASO = 30°.
3) ∠SAC = 60°.
4) ∠SHO = 30°.
Объяснение:
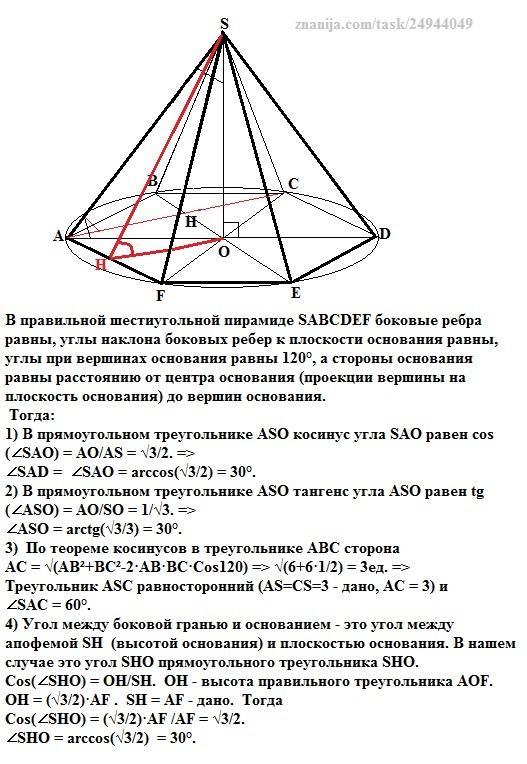
В правильной шестиугольной пирамиде SABCDEF боковые ребра равны, углы наклона боковых ребер к плоскости основания равны, углы при вершинах основания равны 120°, а стороны основания равны расстоянию от центра основания (проекции вершины на плоскость основания) до вершин основания.
Тогда:
1) В прямоугольном треугольнике АSО косинус угла SAO равен сos(∠SAO) = АО/AS = √3/2. =>
∠SAD = ∠SAO = arccos(√3/2) = 30°.
2) В прямоугольном треугольнике АSО тангенс угла АSO равен tg(∠ASO) = АО/SO = 1/√3. =>
∠ASO = arctg(√3/3) = 30°.
3) По теореме косинусов в треугольнике АВС сторона
АС = √(АВ²+ВС²-2·АВ·ВС·Cos120) => √(6+6·1/2) = 3ед. =>
Треугольник АSС равносторонний (AS=CS=3 - дано, АС = 3) и
∠SAC = 60°.
4) Угол между боковой гранью и основанием - это угол между апофемой SH (высотой основания) и плоскостью основания. В нашем случае это угол SHO прямоугольного треугольника SHO.
Cos(∠SHO) = OH/SH. OH - высота правильного треугольника AOF.
OH = (√3/2)·AF . SH = AF - дано. Тогда
Cos(∠SHO) = (√3/2)·AF /AF = √3/2.
∠SHO = arccos(√3/2) = 30°.
1) ∠SAD = 30°.
2) ∠ASO = 30°.
3) ∠SAC = 60°.
4) ∠SHO = 30°.
Объяснение:
В правильной шестиугольной пирамиде SABCDEF боковые ребра равны, углы наклона боковых ребер к плоскости основания равны, углы при вершинах основания равны 120°, а стороны основания равны расстоянию от центра основания (проекции вершины на плоскость основания) до вершин основания.
Тогда:
1) В прямоугольном треугольнике АSО косинус угла SAO равен сos(∠SAO) = АО/AS = √3/2. =>
∠SAD = ∠SAO = arccos(√3/2) = 30°.
2) В прямоугольном треугольнике АSО тангенс угла АSO равен tg(∠ASO) = АО/SO = 1/√3. =>
∠ASO = arctg(√3/3) = 30°.
3) По теореме косинусов в треугольнике АВС сторона
АС = √(АВ²+ВС²-2·АВ·ВС·Cos120) => √(6+6·1/2) = 3ед. =>
Треугольник АSС равносторонний (AS=CS=3 - дано, АС = 3) и
∠SAC = 60°.
4) Угол между боковой гранью и основанием - это угол между апофемой SH (высотой основания) и плоскостью основания. В нашем случае это угол SHO прямоугольного треугольника SHO.
Cos(∠SHO) = OH/SH. OH - высота правильного треугольника AOF.
OH = (√3/2)·AF . SH = AF - дано. Тогда
Cos(∠SHO) = (√3/2)·AF /AF = √3/2.
∠SHO = arccos(√3/2) = 30°.
0
·
Хороший ответ
4 апреля 2023 06:23
Остались вопросы?
Еще вопросы по категории Геометрия
Построить угол 15 градусов и 120 градусов...
Нужно найти производную функции помогите пожалуйста...
Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 3 и 4, и боковым ребром, равным 5....
в Равнобедренном треугольнике один из углов равен 120 градусов, а основание - 12 см. Найдите высоту, проведённую к боковой стороне. Очень надоо!!!!!!...
1)Даны координаты трех вершин параллелограмма ABCD:А(-6;-4;0),В(6;-6;2),С(10;0;4). Найдите координаты точки D и угол между векторами AC и BD. 2)Даны к...