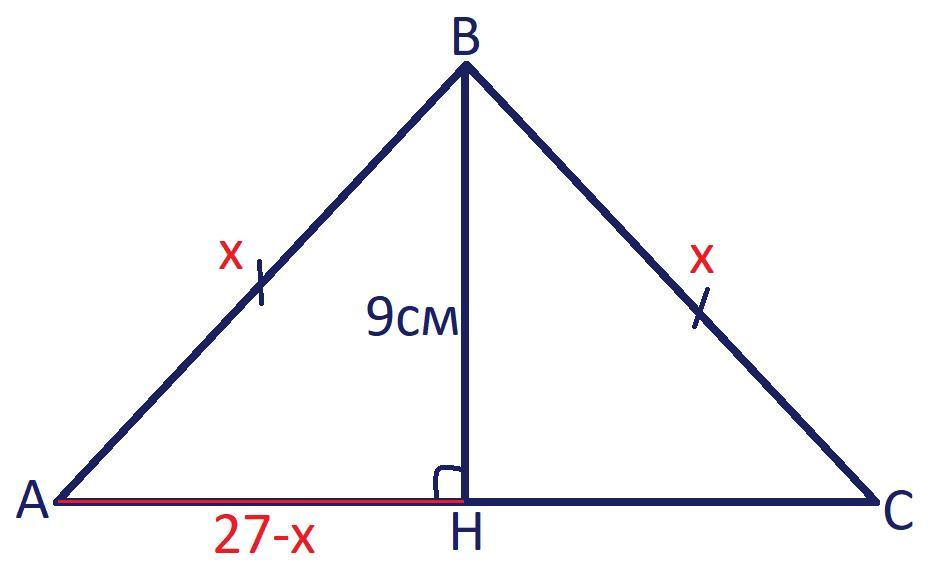
найдите стороны равнобедренного треугольника, если его периметр =54 см, а высота, проведенная к основанию, - 9 см

1 ответ

Посмотреть ответы

Megamozg

2205

Дано: △ABC - равнобедренный (AB=CB); BH - высота; BH = 9см; P(ABC) = 54см.
Найти: AB, BC, AC.
Решение:
Пусть AB = x см.
P(ABC) = AB+BC+AC;
AC = P(ABC)-2·AB;
AC = 54-2x см.

Высота равнобедренного треугольника, проведённая к его основанию, является так же медианой.

⇒ AH = HC = AC:2 = (54-2x):2 = 27-x см;
△AHB - прямоугольный (∠H=90°), тогда по теореме Пифагора получим:
AB² = AH²+BH²;
x² = (27-x)²+9²;
x² = 27²-54x+x²+9²;
54x = 3²·9²+9² = 10·81;
54x = 2·5·3·27;
x = $\dfrac =3\cdot 5=15$
AB = 15см;
BC = AB = 15см;
AC = 54-2·15 = 54-30 = 24 см.
Ответ: 15см, 15см и 24см.

Хороший ответ

4 апреля 2023 08:36

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Докажите, что в равнобедренной трапеции углы при каждом основании равны.... Осевое сечение конуса - прямоугольный треугольник, периметр которого равен Р. Найдите площадь полной поверхности конуса. ... В ромбе ABCD угол A равен 60,AB=6 см.Из вершины B на стороны AD и CD проведены перпендикуляры BM и BK соответственно.Чему равна сумма длин отрезков MD... Катеты прямоугольного треугольника относятся как 3:4 , а гипотенуза равна 15 см,найти периметр треугольника... угол, противолежащий основанию AC равнобедренного треугольника ABC, равен 120 градусов. Боковая сторона BC равна 14см. Чему равен радиус окружности, о...