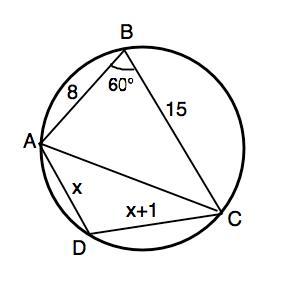
В окружность вписан четырехугольник со сторонами 8 и 15 см а угол между ними равен 60 градусам найдите две другие стороны если одна сторона на 1 см больше другой

1 ответ

Посмотреть ответы

DevAdmin

1720

Ответ: 7 см, 8 см.
Объяснение: Четырехугольник может быть вписан в окружность только тогда, когда сумма его противоположных углов равна 180°.⇒ Если угол АВС=60°, то угол АDC=120°.
Пусть АВ=8 см, ВС=15 см.
По т.косинусов из ∆ АВС диагональ АВСD АС²=AB²+BC²-2•AB•BC•cos60°
АС²=8²+15²-2•8•15•0,5⇒
AC²=169
В ∆ АDC примем АD=x, DC=х+1.
cos120°=-cos60°=(-0,5)
По т.косинусов АС²=x²+(x+1)²-2•x•(x+1)•(-o,5), откуда
169=3x²+3x+1 ⇒
3x²+3x-168=0
Решив квадратное уравнение, получим х₁=7, х₂=-8 (не подходит). ⇒
АD=x=7 см, CD=7 см+1=8 см

Хороший ответ

4 апреля 2023 11:02

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Один из углов образовавшихся при пересечении двух прямых ,равен 21 градус.Найдите остальные углы.Пожалуйста полное решение с объяснением:)... Биссектриса равностороннего треугольника равна 15√3. найти его сторону... Конус получается при вращении равнобедренного прямоугольного треугольника abc вокруг катета, равного 6. Найдти площадь полной поверхности ... Начертите неравнобедренный треугольник ABC с верхней вершиной B. Проведите из венршины B медиану, а из вершины A- биссектрису... На боковых сторонах равнобедренного треугольника ABC отложены равные отрезки BM и BN . BD – медиана треугольника. Докажите, что MD=ND...