Найдите радиус окружности, вписанной в прямоугольную трапецию. если основания равны 3 и 6

1 ответ

Посмотреть ответы

DevAdmin

1720

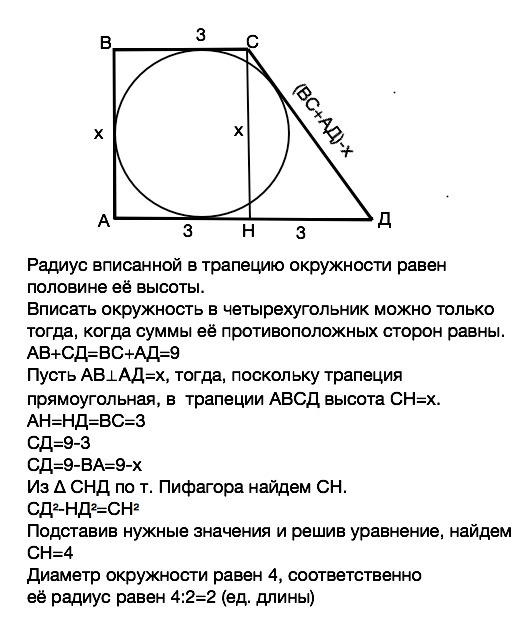
Радиус вписанной в трапецию окружности равен половине её высоты.
Вписать окружность в четырехугольник можно только тогда, когда суммы её противоположных сторон равны.
АВ+СД=ВС+АД=9
Пусть АВ⊥АД=х, тогда, поскольку трапеция прямоугольная, в трапеции АВСД высота СН=АВ=х.
АН=НД=ВС=3
СД=9-ВА=9-х
Из ∆ СНД по т. Пифагора найдем СН.
СД² -НД² =СН²
Подставив нужные значения и решив уравнение, найдем СН=4
Диаметр окружности равен 4, соответственно
её радиус равен 4:2=2

Хороший ответ

4 апреля 2023 11:23

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Геометрия 7 класс. Отрезки АС и ВД пересекаются. Докажите, что АВ+СД<АС+ВД помогите решить, пожалуйста.... Сколько сторон имеет выпуклый многоугольник если сумма его углов его 2160... два велосипедиста одновременно отправляются в 100-километровый пробег. Первый едет со скоростью на 15 км / ч большей, чем второй, и прибывает к финишу... Дан угол 40 градусов найти углы:1,2,3,4,5,6,7... Постройте равнобедренный треугольник, у которого основание в два раза меньше данного отрезка, а боковая сторона равна данному отрезку....