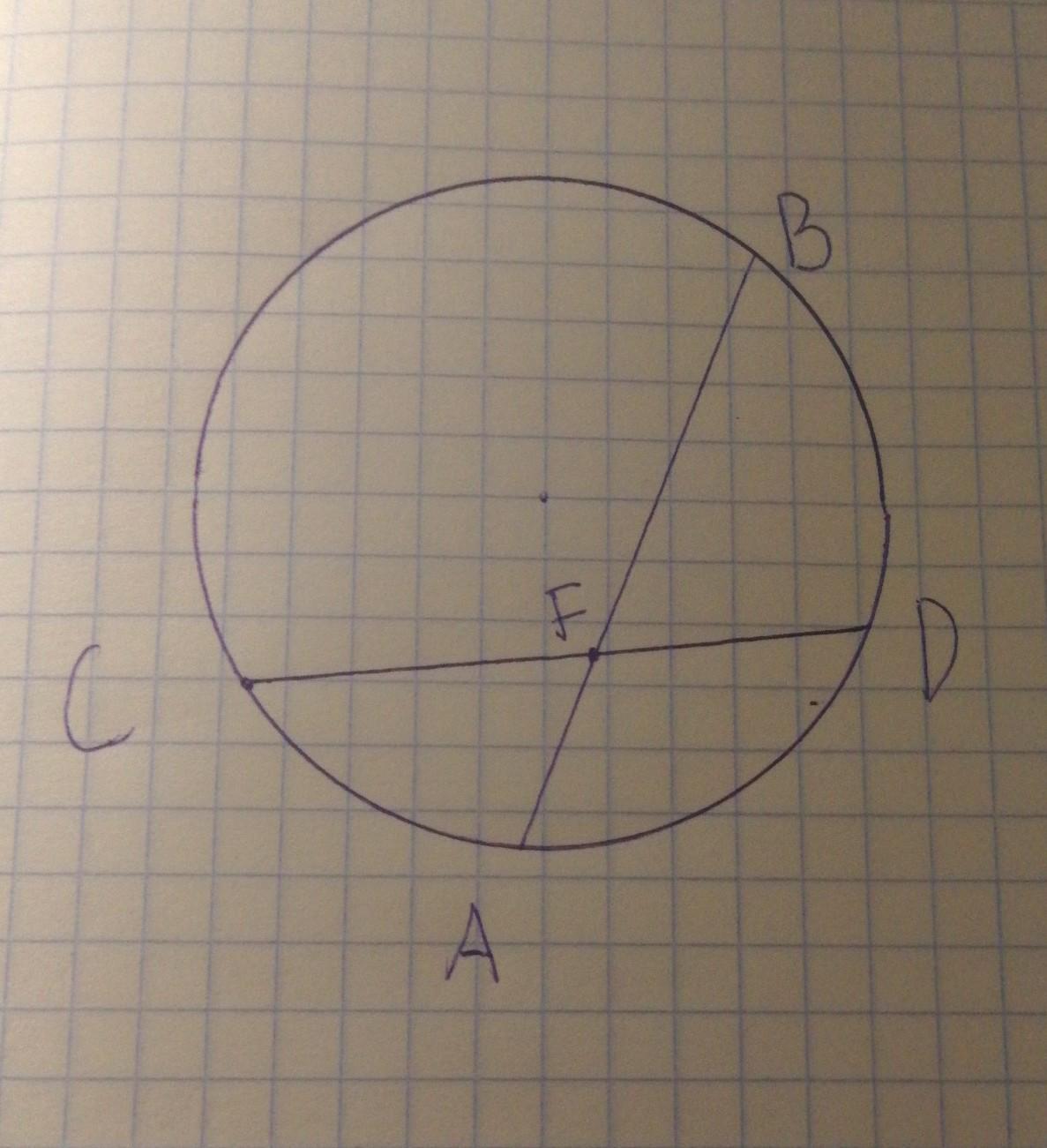
Хорды AB и CD пересекаются в точке F так, что BF =16см, AF=4см, CF=DF. найдите CDПожалуйста срочно

1 ответ

Посмотреть ответы

DevAdmin

1720

1. Воспользуемся тем фактом, что произведения отрезков пересекающихся хорд равны, т.е. CF × DF = AF × BF.
2. Так как по условию CF = DF, то из п. 1 следует, что CF^2 = AF × DF => CF = корень = корень = 8 см.
3. Т.к. CD = CF + DF, то CD = 2CF = 16 см.

Ответ: CD = 16 см.

Хороший ответ

4 апреля 2023 11:50

Остались вопросы?

Найти нужный

Еще вопросы по категории Геометрия

Верно ли что Если прямая перпендикулярна двум сторонам треугольника, то она перпендикулярна плоскости треугольника.... основанием прямой треугольной призмы abca1b1c1 является равнобедренный треугольник abc, в котором ab = bc = 10, ac = 16. боковое ребро призмы равно 12... Найдите объем многогранника,вершинами которого являются точки A, B, C1, Dпрямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB=15,AD=5, AA1=1.... Даны три вершины параллелограмма ABCD: B(-1; 1), C(2; 3), D( 2;-3 ). Найдите координаты вершины А.... Сформулируйте утверждение, обратное следующему: "Если один из смежных углов-острый, то другой-тупой"...

Хорды AB и CD пересекаются в точке F так, что BF =16см, AF=4см, CF=DF. найдите CDПожалуйста срочно​

Хорды AB и CD пересекаются в точке F так, что BF =16см, AF=4см, CF=DF. найдите CDПожалуйста срочно